Seja dada por:
Onde a série do 2º membro é a série de Fourier de
- Prove que é contínua e esboce o gráfico.
Passo 1
Boom galerinha, para todo x e para todo nós temos que:
Levando em consideração nosso
Segundo o Critério M de Weierstrass a série será uniformemente convergente, certo?
E se lembramos do Teorema 1 da seção 7.4 se a série convergir uniformemente ela é contínua!!
Se:
Nós podemos esboçar o gráfico:
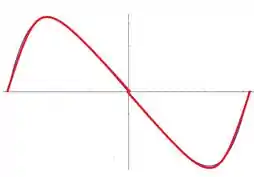
De boas, não foi?