5. Sejam e duas funções definidas em e deriváveis até a ordem, cujos gráficos têm os seguintes aspectos.
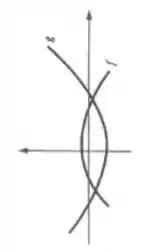
Existe equação do tipo
Com e contínuas em , que admita ambas as funções e como soluções? Explique.
Sugestão: Veja Exercício 4.
Passo 1
No problema anterior, provamos que se existe dois pontos consecutivos e onde uma solução zera duas vezes, a outra função deve passar pelo menos uma vez no interior de e .
Veja a função . Ela zera vezes, mas a função passa pelo zero no intervalo onde está se zerando?
Não né? Isso significa que estas duas soluções não podem ser ambas as soluções da EDO no intervalo de definição.
Resposta
Não. Motivo: função não possui zero no intervalo dos zeros da função .