Suponha que a função seja contínua, decrescente e positiva. Prove:
- convergente convergente.
Passo 1
Bom, primeiramente preste atenção no seguinte gráfico:
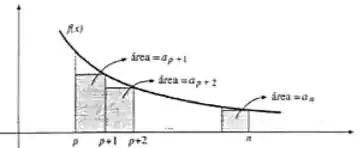
Repare que,
Soma das áreas dos retângulos no intervalo
E
área abaixo da curva no intervalo
Passo 2
Agora, lembre-se da definição de integral de Riemann que diz:
Perceba então que podemos representar da seguinte forma:
Passo 3
Se tomarmos:
Significa dizer:
E então:
Portanto,
Implicando no que queríamos demonstrar:
Resposta
Então, pela Integral de Riemann, mostramos que:
- convergente convergente.