Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Suponha que a função f : 0 , + ∞ → R   seja contínua, decrescente e positiva. Suponha, ainda, que a série ∑ k = 0 + ∞ f ( k )   seja convergente e tenha soma s .

Prove que ∑ k = 0 n f ( k ) è um valor aproximado por falta de s , com erro, em módulo, inferior a ∫ n + ∞ f ( x ) d x .

Passo 1

Bom, primeiramente preste atenção no seguinte gráfico:

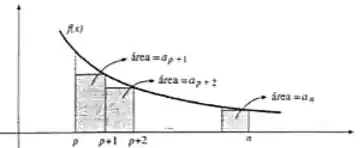
Repare que,

∑ k = 0 n f k = Soma das áreas dos retângulos no intervalo [ 0 ; n ]

E

∫ 0 ∞ f x d x = área abaixo da curva no intervalo [ 0 ; + ∞ )

Passo 2

Repare que, tendo

s = ∑ k = 0 + ∞ f k

E

s n = ∑ k = 0 n f ( k )

Passo 3

Do gráfico, repare que podemos estabelecer a seguinte relação:

∑ k = 0 n f k ≤ ∑ k = 0 + ∞ f k

Repare que podemos ter o seguinte:

∑ k = 0 + ∞ f k 0 - ∑ k = 0 n f k = s - s n = ∑ k = n + 1 + ∞ f k

Pois, é como se tivéssemos tirado uma parte do todo, e então nos sobra um “resto”.

Podemos manipular a relação anterior:

0 < s - s n = ∑ k = n + 1 + ∞ f k ≤ ∫ n ∞ f x d x

Se ficar difícil de visualizar, volte ao gráfico e vê se ajuda.

È mais ou menos a mesma idéia de:

∑ k = 0 n f ( k ) ≤ ∫ 0 n f x d x

Resposta

Ou seja, quando dizemos:

0 < s - s n = ∑ k = n + 1 + ∞ f k ⏟ e r r o ≤ ∫ n ∞ f x d x

Então, temos que s n = ∑ k = 0 n f ( k ) è um valor aproximado para s ,   com erro inferior à ∫ n ∞ f x d x .

Ver Outros Exercícios desse livro