Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.8 - Ex. 3
Verifique se as hipóteses do Teorema de Rolle estão satisfeitas nos intervalos e encontre todos os valores de nesses intervalos que satisfazem a conclusão do teorema.
;
Passo 1
As hipóteses do teorema são que a função deve ser contínua no intervalo fechado e diferenciável no intervalo aberto. Vamos ver o gráfico dessa função no intervalo dado:
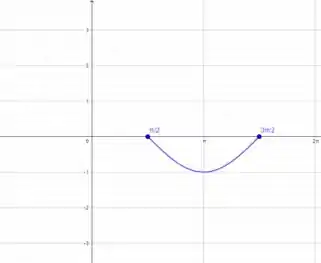
Como não existem “partes quebradas” na função, ou seja, ao desenhar essa função, não precisamos tirar o “lápis do papel”, podemos dizer que ela é contínua (e fica aí essa dica). Além disso, no intervalo aberto não existem “bicos”, logo não há pontos em que a função não seja diferenciável. Se pegarmos a derivada da função: , vemos que ela está definida para todos os valores de dentro dos números reais.
Com isso, nossas hipóteses estão satisfeitas.
Passo 2
Segundo o Teorema de Rolle, as hipóteses sendo verdadeiras, se temos que o valor da função nos extremos do intervalo são iguais, existe ao menos um ponto no meio em que .
Pelo gráfico, vemos que só há um ponto em que isso acontece, vamos descobrí-lo:
Para que o seno seja zero no intervalo , nossa única opção para que isso seja verdade é se:
Pronto, esse ponto está no intervalo dado e a derivada nele é , então esse é o nosso cara!