Quando você abre uma torneira de água quente , a temperatura da água depende do tempo no qual a água está correndo.
- Esboce um gráfico possível de como uma função do tempo que decorreu desde que a torneira foi aberta.
- Descreva como é a taxa de variação de em relação a quando está crescendo
- Esboce um gráfico da derivada de
Passo 1
E aí, tudo bem?! Nesse problema temos uma situação da vida real, abrimos uma torneira de água quente e a temperatura da água vai variar com o tempo.
Sabendo disso a gente precisa, na letra (a), esboçar um gráfico da temperatura versus o tempo . Na letra (b) a gente falar sobre a taxa de variação de a medida que o tempo passa e na letra (c) vamos pegar todo o raciocínio da letra (b) e colocar em um gráfico de versus .
A princípio pra resolver esse problema a gente só precisa ter em mente que a derivada/taxa de variação de um ponto da função é a inclinação da reta tangente nesse ponto. Mas antes de colocar a mão na massa eu tenho uma coisa muito importante pra te falar!

Pra a gente aqui no Brasil o aquecimento de água é elétrico, mas quando falamos de torneira com água quente provavelmente o aquecimento vai ser a gás com aquele aquecedor que faz a combustão e vai aquecendo a água a medida que ela passa no cano por dentro do aquecedor. Certo?!
Poréeeem, esse é um livro americano que é traduzido, e essa questão leva em consideração o sistema de aquecimento de água mais comum nos EUA.
Beleza, mas como que é esse sistema?!
Lá eles usam uma caldeira, que aquece um volume de água em uma espécie de depósito e aí quando acaba essa água quente tem que esperar um tempinho pra aquecer mais!
É por isso que as vezes em filmes ou séries americanas a gente tem situações de alguém reclamando que outra pessoa ficou muito tempo no banho e acabou a água quente!
Agora vamos ao que interessa!
Passo 2
Beleza, agora pra desenhar o gráfico a gente tem que pensar fisicamente no que acontece a partir do momento que a gente abre a torneira!
Antes da gente abrir a torneira tem uma água parada no cano, então podemos imaginar que essa água tem temperatura próxima a ambiente, só um pouquinho mais quente. Afinal inicialmente ela tava quente e com o passar do tempo foi entrando em equilíbrio com a temperatura ambiente. Essa suposição faz sentido porque a gente abre a torneira com alguma frequência, mas também poderíamos supor que a torneira esta a muuuuitas horas sem ser ligada, então a temperatura seria ambiente! Sacou?!
Vamos supor que essa temperatura seja:
Esse é o nosso primeiro ponto!
Em seguida a água aquecida começa a passar e a temperatura aumenta, vamos supor que ela seja:
Esse é o nosso segundo ponto!
Como a água vem de um depósito com temperatura constante, podemos dizer que a temperatura da torneira vai permanecer contante por um tempo, então:
Depois de um tempo a água do depósito acaba e passamos a ter água em temperatura ambiente, vamos dizer que:
Colocando isso no gráfico:

Tranquilo até aqui?
Passo 3
Agora a gente tem que refletir sobre a taxa de variação da temperatura ao longo do tempo, :
A temperatura inicial da água está próxima da temperatura ambiente por causa da água que estava nos canos. Quando a água do tanque de água quente começa a sair, é grande e positivo quando aumenta para a temperatura da água no tanque.
Na fase seguinte, quando a água sai a uma temperatura constante e alta. Depois de algum tempo, torna-se pequeno e negativo à medida que o conteúdo do tanque de água quente se esgota.
Finalmente, quando a água quente acaba, é novamente 0 quando a água mantém sua temperatura (fria)!
Passo 4
Agora precisamos desenhar o gráfico da derivada ao longo do tempo. Vamos trazer nosso gráfico pra pertinho:
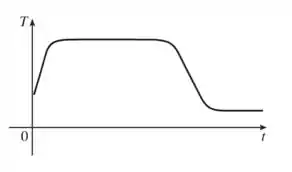
O nosso gráfico é composto por 4 segmentos de retas. Lembra que a derivada é a inclinação da reta tangente a um ponto do gráfico?!
Se o nosso gráfico é uma reta, então essa inclinação é constante. Isso significa que o gráfico da derivada vai ser dividido em 4 partes com retas horizontais. Já falamos basicamente tudo no passo anterior, mas vamos recaptular:
- No primeiro momento temos uma inclinação positiva grande, então teremos um grande;
- Depois não temos nenhuma inclinação, ou seja é igual a zero;
- Quando a água do depósito acaba temos uma inclinação negativa significativa, assim será negativo;
- Finalmente no último momento temos apenas água gelada saindo em uma temperatura constante. Então volta a ser igual a zero.
Juntando essas informações chegamos em:

E aí! o que achou? Responde Aí! 😊
Resposta
a) Esboço do gráfico;
b) A temperatura inicial da água está próxima da temperatura ambiente por causa da água que estava nos canos. Quando a água do tanque de água quente começa a sair, é grande e positivo quando aumenta para a temperatura da água no tanque. Na fase seguinte, quando a água sai a uma temperatura constante e alta. Depois de algum tempo, torna-se pequeno e negativo à medida que o conteúdo do tanque de água quente se esgota. Finalmente, quando a água quente acaba, é novamente 0 quando a água mantém sua temperatura (fria).
c) Esboço do gráfico.