Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 50
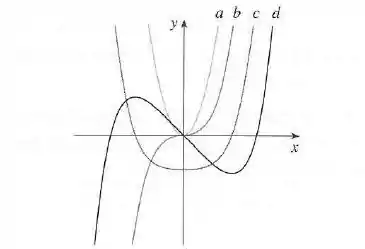
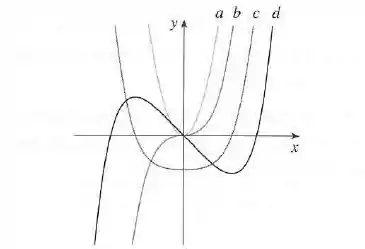
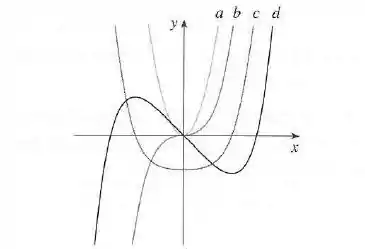
A figura mostra os gráficos de . Identifique cada curva e explique suas escolhas.
Passo 1
Opa, bora lá!
O enunciado nos dá um gráfico com as curvas de uma função e suas 3 primeiras derivadas e a gente precisa identificar quem é quem.
Pra isso vamos lembrar de algumas informações sobre as derivadas:
- Quando uma função é crescente, sua derivada é positiva
- Quando uma função é decrescente, sua derivada é negativa
- Quando uma função tem um ponto de máximo ou mínimo (reta tangente horizontal), sua derivada é nula
Com essas 3 informações vamos analisar o comportamento das 4 curvas.
Passo 2
Vamos analisar:
Quando possui um ponto com reta tangente horizontal, vale 0, quando possui um ponto com reta tangente horizontal vale 0 e, quando possui um ponto com reta tangente horizontal vale 0.
Entãio sera que podemos dizer isso aqui?
Vamos crecar os intervalos de crescimento e decrescimento. Quando cresce, é positiva. Quando decresce, é negativa. Então faz sentido dizer que
Vemos o mesmo comportamento entre e . Quando c cresce (, é positiva. Quando decresce (, é negativa. Então faz sentido dizer que
E como é sempre crescente, sua derivada é sempre positiva!
Maravilha! Tudo fez sentido!
Prontinho!