Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Soma e Produto e Fórmula de Bhaskara

Ver Todos os Exercícios

Teoria

Fala aí! Hoje quero te apresentar o método da soma e produto, um caminho muito prático para encontrar as raízes de equações do segundo grau sem precisar calcular delta, fórmula de Bhaskara e todo aquele lero lero.

⭐ Veja também ⭐

Método da Soma e Produto

Lembre que uma equação do segundo grau tem essa carinha aqui:

A gente costuma padronizar que o coeficiente a multiplica o termo elevado ao quadrado (), o coeficiente b multiplica o termo elevado a 1 () e o c multiplica o termo elevado a zero (como , o coeficiente c fica sozinho).

Uma equação desse tipo pode fornecer até duas raízes reais, não é?

Vamos chamá-las de e .

O método que quero te mostrar diz que as duas raízes da equação obedecem as seguintes relações:

Bora ver um exemplo com números pra deixar isso aí mais claro?

Exemplo: Encontre as raízes da equação x²-7x+12.

Olha só, os nossos coeficientes são:

O método da soma e produto diz que o produto das duas raízes que queremos encontrar é igual a c sobre a.

Beleza, então queremos encontrar dois números reais que, quando multiplicados, resultam em 12. Temos esses carinhas aqui como candidatos às nossas raízes:

Qual será nossa resposta? Descobrimos usando a outra parte do método!

A soma das duas raízes deve ser igual a menos b sobre a.

Não esqueça do jogo de sinais!!!

O raciocínio agora é: dentre os possíveis candidatos que encontramos anteriormente, qual deles também satisfazem essa soma?

A última alternativa satisfaz a soma!
A última alternativa satisfaz a soma!

Os números 3 e 4 satisfazem tanto a soma quanto o produto! Portanto, são as raízes da nossa equação.

Se perdeu em algum momento? Confere esse vídeo aqui, nele te explico tudo isso de um jeito fácil pra você entender 👇

Agora, vamos confirmar nosso resultado pelo método tradicional?

Fórmula de Bhaskara

A fórmula de Bhaskara nos fornece o meio mais tradicional para encontrarmos raízes de funções do segundo grau. A fórmula é a seguinte:

Pera aê! Que que esse triângulo tá fazendo aí? E aquele mais em cima do menos?

Esse cara é o famoso Delta, pode ir se acostumando com ele 😅 Quanto ao sinal de mais em cima do menos, a gente chama de “mais ou menos”, já te mostro como vamos usá-lo.

Para encontrar esse Delta, usamos essa outra equação aqui:

Então você pode começar pelo cálculo do delta e depois substitui o resultado na outra expressão, ou já pode fazer tudo de uma vez só, fica ao seu critério. Se você quiser, pode juntar as duas equações assim:

Bora tentar aquele mesmo exemplo, dessa vez usando Bhaskara.

Exemplo: Encontre as raízes da equação x²-7x+12 pela fórmula de Bhaskara.

Vou fazer passo a passo pra ficar mais fácil de acompanhar.

Lembrando que:

Começamos pelo delta:

Agora a gente substitui isso aí na outra expressão para encontrar as raízes.

Agora aquele mais ou menos entra em ação, a gente faz isso assim: primeiro considera a soma, depois a subtração.

E assim, chegamos no mesmo resultado de antes!!!

Possíveis Valores de Delta

Isso aqui é um detalhe bem importante. Existem três tipos possíveis para o delta:

1º Caso: .

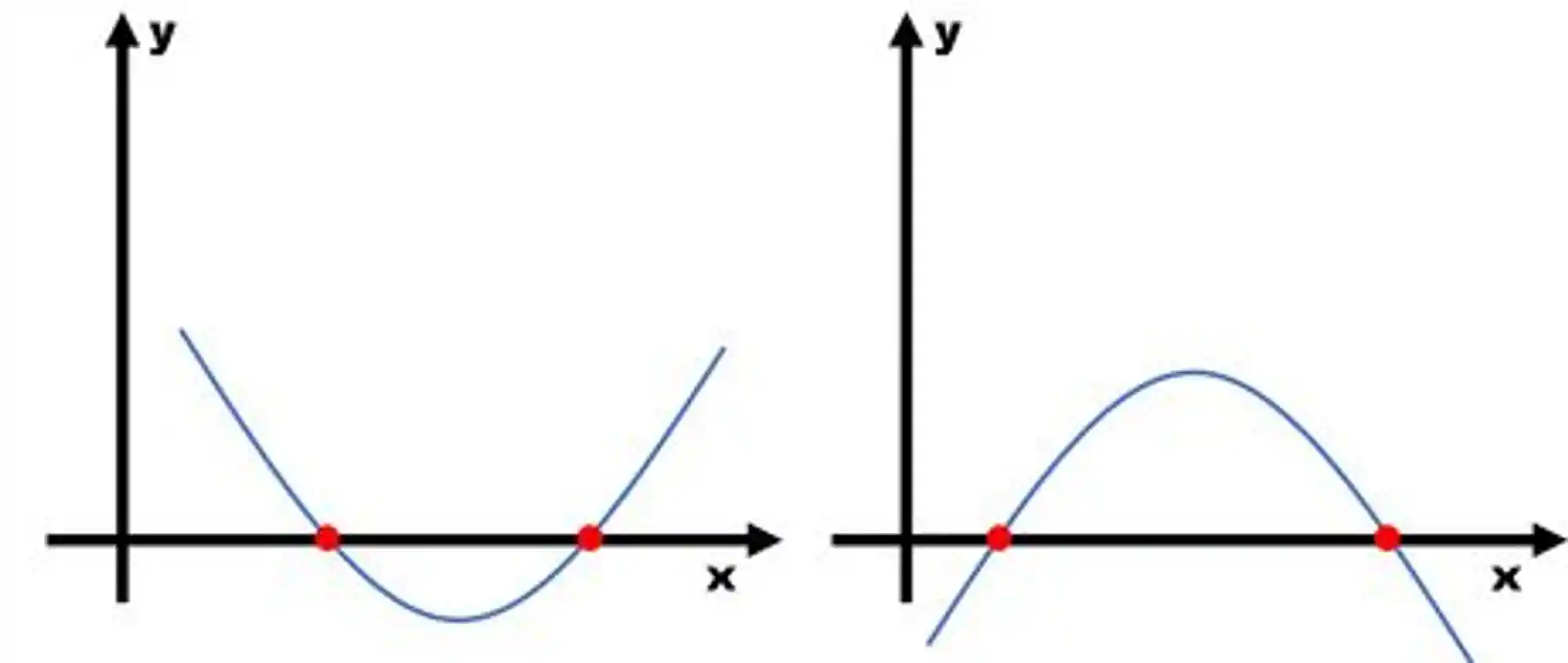
Esse é como o que achamos no exemplo resolvido acima. Nestes casos, a equação possui duas raízes.

Graficamente, teríamos uma função assim:

Interpretação gráfica do delta positivo.
Interpretação gráfica do delta positivo.

2º Caso: .

Pensa aqui: quando você substituir na fórmula:

Com o delta igual a zero:

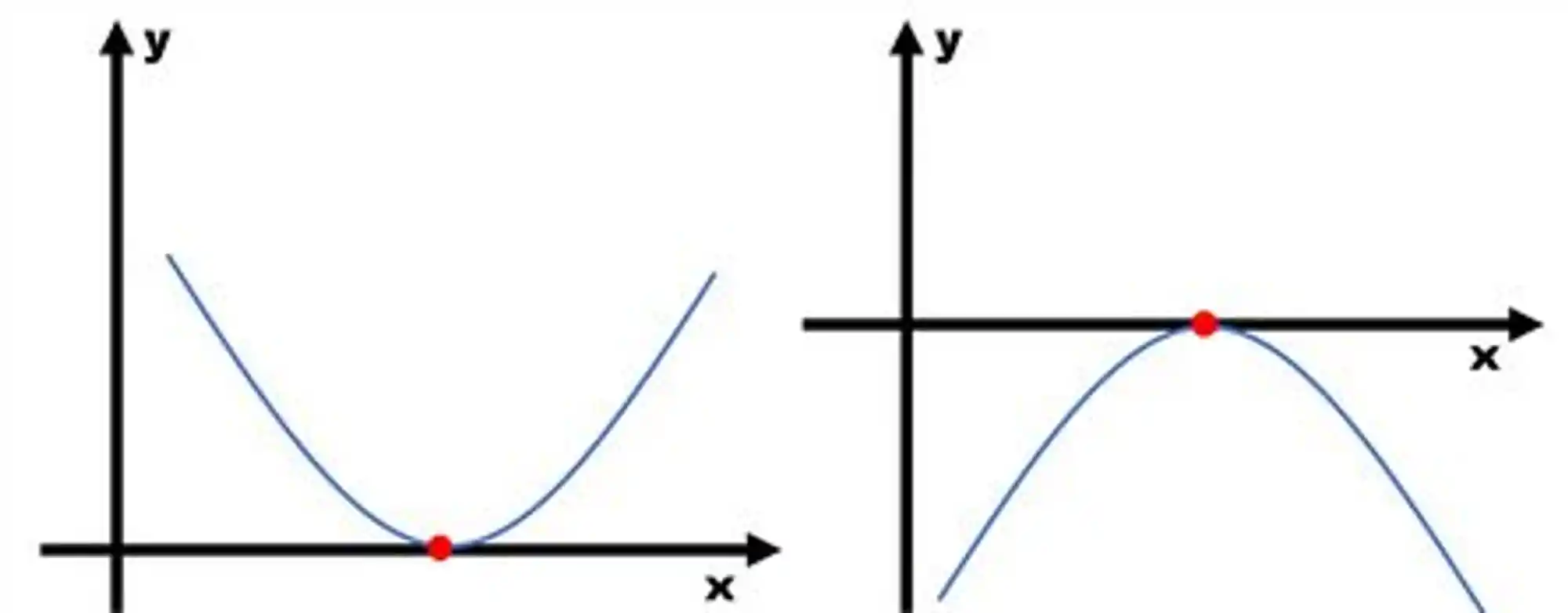
A gente só vai ter uma única raiz!

Graficamente, a função tem uma dessas caras aqui:

Interpretação gráfica do delta nulo.
Interpretação gráfica do delta nulo.

3º Caso: .

Dessa vez, quando você for substituir na fórmula, vai se deparar com a raiz quadrada de um número negativo.

Acontece que não existe solução real para esse problemão aí! Então a gente fala que a função não possui raízes reais.

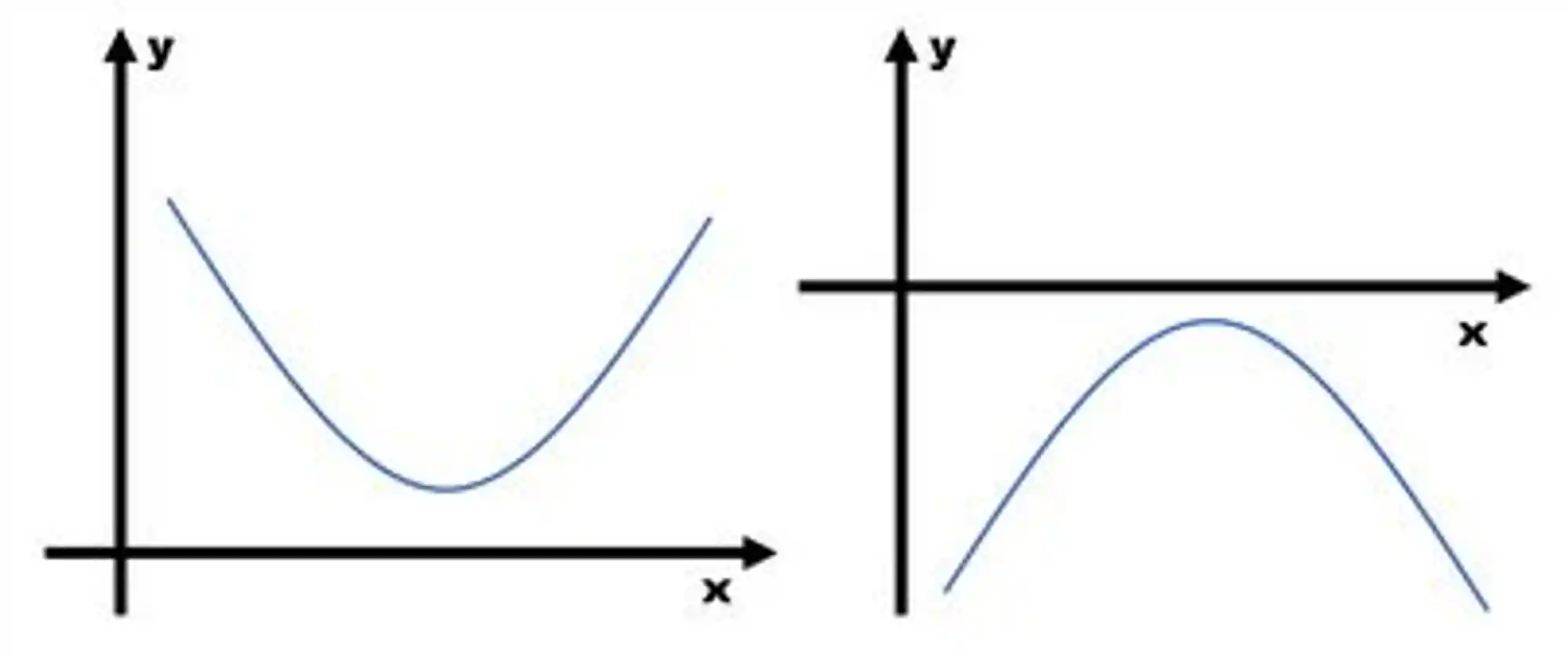
Interpretação gráfica para o delta negativo.
Interpretação gráfica para o delta negativo.

Belezinha? Agora bora praticar bastante pra ficar bem craques nisso aí!

Fórmula de Bhaskara

Possíveis Valores de Delta

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Encontre as raízes das funções abaixo por meio de Bhaskara:

  1. y = x 2 + x - 2
  2. y = x 2 + 2 x - 3

Passo 1

Vamos lembrar que a fórmula de Bhaskara é: - b ± ∆ 2 a

Onde ∆ = b 2 - 4 a c

  1. y = x 2 + x - 2

    2. Nossos coeficientes:

    a = 1

    b = 1

    c = - 2

    Vamos descobrir o valor de delta:

    ∆ = b 2 - 4 a c

    ∆ = 1 2 - 4 1 - 2

    ∆ = 1 + 8 = 9

    Agora descobrindo as raízes:

    - b ± ∆ 2 a

    - 1 ± 9 2 ( 1 ) = - 1 ± 3 2

    Agora vamos abrir a soma (primeira raiz) e depois a subtração (segunda raiz)

    x ' = - 1 + 3 2 = 2 2 = 1

    x " =     - 1 - 3 2 = - 4 2 = - 2

    Passo 2

  2. y = x 2 + 2 x - 3

Nossos coeficientes:

a = 1

b = 2

c = - 3

Vamos descobrir o valor de delta:

∆ = 2 2 - 4 ( 1 ) ( - 3 )

∆ = 4 + 12

∆ = 16

Agora descobrindo as raízes:

- b ± ∆ 2 a

- 2 ± 16 2 ( 1 ) = - 2 ± 4 2

Agora vamos abrir a soma (primeira raiz) e depois a subtração (segunda raiz)

x ' = - 2 + 4 2 = 2 2 = 1

x " =     - 2 - 4 2 = - 6 2 = - 3

Resposta

  1. x ' = 1   e x " =   - 2
  2. x ' = 1   e x " =   - 3

Exercício Resolvido #2

Elaboração Própria

Encontre as raízes das funções abaixo por meio de Bhaskara:

  1. y = - 2 x 2 + 8 x - 8
  2. y = - x 2 + 6 x - 9

Passo 1

Vamos lembrar que a fórmula de Bhaskara é: - b ± ∆ 2 a

Onde ∆ = b 2 - 4 a c

  1. y = - 2 x 2 + 8 x - 8

    2. Nossos coeficientes:

    a = - 2

    b = 8

    c = - 8

    Vamos descobrir o valor de delta:

    ∆ = b 2 - 4 a c

    ∆ = 8 2 - 4 - 2 - 8

    ∆ = 64 - 64 = 0

    Como ∆ = 0 só vai existir uma única raiz: - b ± ∆ 2 a

    x ' = x " = - 8 ± 0 2 ( - 2 ) = - 8 - 4 = 2

    Passo 2

  2. y = - x 2 + 6 x - 9

Nossos coeficientes:

a = - 1

b = 6

c = - 9

Vamos descobrir o valor de delta:

∆ = b 2 - 4 a c

∆ = 6 2 - 4 - 1 - 9

∆ = 36 - 36 = 0

Novamente, temos ∆ = 0 só vai existir uma única raiz: - b ± ∆ 2 a

x ' = x " = - 6 ± 0 2 ( - 1 ) = - 6 - 2 = 3

Resposta

  1. x ' = x " = 2
  2. x ' = x " = 3

Exercício Resolvido #3

Elaboração própria

Encontre as raízes das funções abaixo por meio de Bhaskara:

  1. y = 3 x 2 + 2 x + 1
  2. y = x 2 + 2 x + 3

Passo 1

Vamos lembrar que a fórmula de Bhaskara é: - b ± ∆ 2 a

Onde ∆ = b 2 - 4 a c

  1. y = 3 x 2 + 2 x + 1

    2. Nossos coeficientes:

    a = 3

    b = 2

    c = 1

    Vamos descobrir o valor de delta:

    ∆ = 2 2 - 4 3 ( 1 )

    ∆ = 4 - 12

    ∆ = - 8

    Quando temos ∆ < 0 , não temos raízes.

    Passo 2

  2. y = x 2 + 2 x + 3

Nossos coeficientes:

a = 1

b = 2

c = 3

Vamos descobrir o valor de delta:

∆ = 2 2 - 4 1 ( 3 )

∆ = 4 - 12

∆ = - 8

Quando temos ∆ < 0 , não temos raizes.

Resposta

  1. Não temos raízes reais
  2. Não temos raízes reais

Exercício Resolvido #4

DANTE, Luiz Roberto. Tudo é matemática – 9 ano. São Paulo, SP:Atica,2009 pp.107 (adaptado)

Sem fazer gráfico, registre se a parábola cruza o eixo x em um único ponto, em dois pontos ou se não cruza o eixo x

  1. y = - 2 x 2 + 8 x - 8
  2. y = 2 x 2 - 1
  3. y = x 2 + 1
  4. y = - 3 x 2 + 5 x

Passo 1

Nesse exercício o que vai nos ajudar é o delta, se temos:

∆   > 0 o eixo x é cortado em dois pontos

∆   = 0 o eixo x é cortado em uns pontos

∆   < 0 não cruza o eixo x

  1. y = - 2 x 2 + 8 x - 8

    2. Nossos coeficientes:

    a = - 2

    b = 8

    c = - 8

    Vamos descobrir o valor de delta:

    ∆ = b 2 - 4 a c

    ∆ = 8 2 - 4 - 2 - 8

    ∆ = 64 - 64 = 0

    Como ∆   = 0 o eixo x é cortado em um único ponto.

  2. y = 2 x 2 - 1

    3. Nossos coeficientes:

    a = 2

    b = 0

    c = - 1

    Vamos descobrir o valor de delta:

    ∆ = b 2 - 4 a c

    ∆ = 0 2 - 4 2 - 1

    ∆ = 0 + 8 = 8

    Como, ∆   > 0 o eixo x é cortado em dois pontos.

    Passo 2

  3. y = x 2 + 1

    4. Nossos coeficientes:

    a = 1

    b = 0

    c = 1

    Vamos descobrir o valor de delta:

    ∆ = b 2 - 4 a c

    ∆ = 0 2 - 4 1 1

    ∆ = 0 - 4 = - 4

    Como ,   ∆   < 0 não cruza o eixo x.

  4. y = - 3 x 2 + 5 x

Nossos coeficientes:

a = - 3

b = 5

c = 0

Vamos descobrir o valor de delta:

∆ = b 2 - 4 a c

∆ = 5 2 - 4 - 3 0

∆ = 25 + 0 = 25

Como, ∆   > 0 o eixo x é cortado em dois pontos.

Resposta

  1. Um ponto
  2. Dois pontos
  3. Não cruza
  4. Dois pontos

Exercício Resolvido #5

DANTE, Luiz Roberto. Tudo é matemática -9°ano.  São Paulo, SP: Ática, 2009. pp.107

Determine os pontos se existirem, nos quais a parábola intersecta os eixos y e x:

  1. y = x 2 - 4 x + 4
  2. y = x 2 + 2 x - 3
  3. y = x 2 - 6 x + 9
  4. y = x 2 - 4

Passo 1

Vamos lembrar que para intersectar o eixo y, precisamos que x = 0 e para intersectar o eixo x precisamos de y = 0 . Assim, vamos analisar cada função.

  1. y = x 2 - 4 x + 4

    2. Eixo y:

    Precisamos de x = 0 , assim vamos substituir na nossa função.

    y = ( 0 ) 2 - 4 ( 0 ) + 4

    y = 4

    Assim a função intercepta o eixo y em ( 0,4 )

    Eixo x:

    Agora precisamos que y = 0 , ou seja:

    x 2 - 4 x + 4 = 0

    Para resolver, vamos usar Bhaskara, onde: a = 1

    b = - 4

    c = 4

    O nosso delta é encontrado da seguinte forma:

    ∆ = b 2 - 4 a c

    ∆ = ( - 4 ) 2 - 4 ( 1 ) ( 4 )

    ∆ = 16 - 16 = 0

    Existe apenas uma raiz:

    x ' = x " = - b ± ∆ 2 a = - b ± 0 2 a = - b 2 a

    x ' = x " = - ( - 4 ) 2 ( 1 ) = 2

    Assim a função intercepta o eixo x em ( 2 , 0 )

    Passo 2

  2. y = x 2 + 2 x - 3

    3. Eixo y:

    Precisamos de x = 0 , assim vamos substituir na nossa função.

    y = ( 0 ) 2 + 2 0 - 3

    y = - 3

    Assim a função intercepta o eixo y em ( 0   3 )

    Eixo x:

    Agora precisamos que y = 0 , ou seja:

    x 2 + 2 x - 3 = 0

    Para resolver, vamos usar Bhaskara, onde: a = 1 .

    b = 2

    c = - 3

    Calculando o delta:

    ∆ = b 2 - 4 a c

    ∆ = ( 2 ) 2 - 4 ( 1 ) ( - 3 )

    ∆ = 4 + 12 = 16

    Existem apenas duas raízes:

    x ' = - b + ∆ 2 a

    x ' = - 2 + 16 2 ( 1 ) = - 2 + 4 2 = 2 2 = 1

    A segunda raiz:

    x ' ' = - b - ∆ 2 a

    x ' ' = - 2 - 16 2 1 = - 2 - 4 2 = - 6 2 = - 3

    Assim a função intercepta o eixo x em ( 1 , 0 ) e ( - 3,0 )

    Passo 3

  3. y = x 2 - 6 x + 9

    4. Eixo y:

    Precisamos de x = 0 , assim vamos substituir na nossa função.

    y = ( 0 ) 2 - 6 ( 0 ) + 9

    y = 9

    Assim a função intercepta o eixo y em ( 0 , 9 )

    Eixo x:

    Agora precisamos que y = 0 , ou seja:

    x 2 - 6 x + 9 = 0

    Para resolver, vamos usar Bhaskara, onde: a = 1 .

    b = - 6

    c = 9

    O nosso delta é encontrado da seguinte forma:

    ∆ = b 2 - 4 a c

    ∆ = ( - 6 ) 2 - 4 ( 1 ) ( 9 )

    ∆ = 36 - 3 6 = 0

    Existe apenas uma raiz:

    x ' = x " = - b ± ∆ 2 a = - b ± 0 2 a = - b 2 a

    x ' = x " = - ( - 6 ) 2 ( 1 ) = 3

    Assim a função intercepta o eixo x em ( 3 , 0 )

    Passo 4

  4. y = x 2 - 4

Eixo y:

Precisamos de x = 0 , assim vamos substituir na nossa função.

y = ( 0 ) 2 - 4

y = - 4

Assim a função intercepta o eixo y em ( 0   4 )

Eixo x:

Agora precisamos que y = 0 , ou seja:

x 2 - 4 = 0

Para resolver, vamos usar Bhaskara, onde: a = 1

b = 0

c = - 4

Calculando o delta:

∆ = b 2 - 4 a c

∆ = ( 0 ) 2 - 4 ( 1 ) ( - 4 )

∆ = 0 + 1 6 = 16

Existem apenas duas raízes:

x ' = - b + ∆ 2 a

x ' = 0 + 16 2 ( 1 ) = 0 + 4 2 = 4 2 = 2

A segunda raiz:

x ' ' = - b - ∆ 2 a

x ' ' = 0 - 16 2 1 = 0 - 4 2 = - 4 2 = - 2

Assim a função intercepta o eixo x em ( 2 , 0 ) e ( - 2 , 0 )

Resposta

  1. Eixo y: ( 0,4 )

    2. Eixo x:   ( 2,0 )

  2. Eixo y: ( 0 ,   - 3 )

    3. Eixo x:   ( - 3 , 0 ) e 1,0

  3. Eixo y: ( 0 , 9 )

    4. Eixo x:   ( 3 , 0 )

  4. Eixo y: ( 0 ,   - 4 )

Eixo x:   ( 2,0 ) e ( - 2,0 )

Exercício Resolvido #6

Elaboração Própria

Pelo método soma e produto, encontre as raízes: f x = x 2 - 6 x + 5

Passo 1

Os nossos coeficientes são:

a = 1

b = - 6

c = 5

Usando a regrinha da multiplicação:

x ' ∙ x ' ' = c a

x ' ∙ x ' ' = 5 1 = 5

Ou seja, descobrimos que se multiplicamos nossas duas raízes, temos o valor de 5 .

Agora, vamos pensar em que números multiplicados satisfazem essa equação:

5 × 1 = 5

2,5 × 2 = 5

( - 5 ) × - 1 = 5

Passo 2

Agora, vamos usar a fórmula da soma:

x ' + x ' ' = - b a

x ' + x ' ' = - - 6 1 = 6  

Assim, sabemos que as raízes somadas resultam 6 , vamos pegar os valores que multiplicamos antes e ver em qual deles a soma dá · .

5 + 1 = 6

2,5 + 2 = 4,5

- 5 + - 1 = - 6

Assim temos que as raízes é o que satisfez tanto a soma como produto:

Produto x ' ∙ x ' ' = 5 :

5 × 1 = 5

Soma:   x ' + x ' ' = 6

5 + 1 = 6

Assim, x ' = 5 e x ' ' = 1

Resposta

x ' = 5

  x ' ' = 1

Exercício Resolvido #7

Elaboração própria

Pelo método soma e produto, encontre as raízes: f x = 3 x 2 - 8 x - 3

Passo 1

Os nossos coeficientes são:

a = 3

b = - 8

c = - 3

Usando a regrinha da multiplicação:

x ' ∙ x ' ' = c a

x ' ∙ x ' ' = - 3 3 = - 1

Ou seja, descobrimos que se multiplicamos nossas duas raízes, temos o valor de - 1 .

Agora, vamos pensar em que números multiplicados satisfazem essa equação:

1 × - 1 = - 1

1 2 × - 2 = - 1

3 × - 1 3 = - 1

Passo 2

Agora, vamos usar a fórmula da soma:

x ' + x ' ' = - b a

x ' + x ' ' = - - 8 3 = 8 3  

Assim, sabemos que as raízes somadas resultam 8 3 , vamos pegar os valores que multiplicamos antes e ver em qual deles a soma dá · .

1 + - 1 = 0

1 2 + ( - 2 ) = - 3 2

3 + - 1 3 = 8 3

Assim temos que as raízes é o que satisfez tanto a soma como produto:

Produto x ' ∙ x ' ' = - 1 :

3 × - 1 3 = - 1

Soma:   x ' + x ' ' = 8 3

3 + - 1 3 = 8 3

Assim, x ' = 3 e x ' ' = - 1 3

Resposta

x ' = 3

  x ' ' = - 1 3

Exercício Resolvido #8

DANTE, Luiz Roberto. Matemática- contexto e aplicações. ED. Renovada. São Paulo, SP: ática, 2010. pp.154

Seja f : R → R ,a função definida por f x = 4 x 2 - 4 x + 3 . Determine x se houver, para que se tenha:

  1. f x = 2
  2. f ( x ) = 3
  3. f x = - 1

Passo 1

  1. Se queremos f x = 2 , vamos substituir:

f x = 4 x 2 - 4 x + 3

2 = 4 x 2 - 4 x + 3

Resolvendo:

4 x 2 - 4 x + 3 - 2 = 0

4 x 2 - 4 x + 1 = 0

Para resolver essa a equação, vamos usar Bhaskara, nossos coeficientes:

a = 4

b = - 4

c = 1

Fazendo o delta:

∆ = b 2 - 4 a c

∆ = - 4 2 - 4 ( 4 ) ( 1 )

∆ = 16 - 16 = 0

Teremos uma raiz:

x ' = x ' ' = - b ± ∆ 2 a = - b ± 0 2 a = - b 2 a

x ' = x ' ' = - ( - 4 ) 2 ( 4 ) = 1 2

Assim, x = 1 2

Passo 2

  1. Se queremos f x = 3 , vamos substituir:

f x = 4 x 2 - 4 x + 3

3 = 4 x 2 - 4 x + 3

Resolvendo:

4 x 2 - 4 x + 3 - 3 = 0

4 x 2 - 4 x = 0

Para resolver essa a equação, vamos usar Bhaskara, nossos coeficientes:

a = 4

b = - 4

c = 0

Fazendo o delta:

∆ = b 2 - 4 a c

∆ = - 4 2 - 4 ( 4 ) ( 0 )

∆ = 16

Teremos duas raízes:

x ' = - b + ∆ 2 a

x ' = - - 4 + 4 2 ( 4 ) = 1

e

x ' ' = - b - ∆ 2 a

x ' ' = - - 4 - 4 2 ( 4 ) = 0

Assim, x ' = 1 e x ' ' = 0

Passo 3

  1. Se queremos f x = - 1 , vamos substituir:

f x = 4 x 2 - 4 x + 3

- 1 = 4 x 2 - 4 x + 3

Resolvendo:

4 x 2 - 4 x + 3 + 1 = 0

4 x 2 - 4 x + 4 = 0

Para resolver essa a equação, vamos usar Bhaskara, nossos coeficientes:

a = 4

b = - 4

c = 4

Fazendo o delta:

∆ = b 2 - 4 a c

∆ = - 4 2 - 4 ( 4 ) ( 4 )

∆ = 16 - 64 = - 48

Como nosso delta é negativo, não temos solução real;

Resposta

  1. x = 1 2
  2. x ' = 1 e x ' ' = 0
  3. Sem solução

Exercício Resolvido #9

DANTE, Luiz Roberto. Matemática- contexto e aplicações. ED. Renovada. São Paulo, SP: ática, 2010. pp.179

A reta gráfico da função f x = 3 x - 1 , e a parábola, gráfico da função g x = x 2 - x + 2 , têm pontos comuns? Se tiverem, descubram quais.

Passo 1

Queremos saber quando os gráficos se cruzam, ou seja, quando ocorre isso aqui:

f x = g ( x )

Igualando:

3 x - 1 = x 2 - x + 2

x 2 - x - 3 x + 2 + 1 = 0

x 2 - 4 x + 3 = 0

Vamos aplicar Bhaskara:

Nossos coeficientes:

a = 1

b = - 4

c = 3

Vamos descobrir o valor de delta:

∆ = ( - 4 ) 2 - 4 1 ( 3 )

∆ = 16 - 12

∆ = 4

Agora, vamos calcular as raízes:

x ' = - b + ∆ 2 a

x ' = - - 4 + 2 2 ( 1 ) = 3

e

x ' ' = - b - ∆ 2 a

x ' ' = - - 4 - 2 2 ( 1 ) = 1

Assim, se encontram em x = 3 e x = 1 .

Pra fechar com chave de ouro, como calculamos os valores de x tais que f x = g ( x )

Então,

f x = g x = 8 , quando x = 3   e f x = g x = 2 quando x = 1 . Show de bola?!

Resposta

  f x = g x = 8 quando x = 3   E f x = g x = 2 quando x = 1 .

Exercício Resolvido #10

A área de um círculo é dada em função da medida r do raio, ou seja, S = f r = π r 2 , que é uma função quadrática. Considerando π = 3,14 , calcule:

  1. S quando r = 5     c m
  2. r quando S = 200,96

Passo 1

  1. Vamos substituir r = 5     c m

f r = π r 2

f 5 = π 5 2

f 5 = 78.5

Assim, S = 78.5   c m 2

Passo 2

  1. Vamos substituir S = 200,96 :

S = π r 2

200,96 = π r 2

Poderíamos igualar a zero e usar Bhaskara, mas é mais fácil, apenas tirar a raiz:

200,96 π = r 2

r 2 = 64

r = 64

r = 8   c m

Resposta

  1. S = 78.5   c m 2
  2. r = 8   c m