Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Introdução à Funções do 2º Grau

Ver Todos os Exercícios

Teoria

Introdução

As funções do 2º grau (também conhecidas como função quadrática) são conhecidas por ter um gráfico na forma de parábola.

Existem diversos exemplos de aplicações onde essas funções são utilizadas no cotidiano, como:

- Cálculos da Física.

- Cálculos Financeiro.

- Taxas de crescimento e decrescimento.

Definição

A função do 2º Grau é dada por:

f x = a x 2 + b x + c

Onde,

a , b e c são números reais R ;

a ≠ 0 ;

Para a , temos dois casos.

Caso 1 – Para a > 0 , temos uma parábola com concavidade para cima.

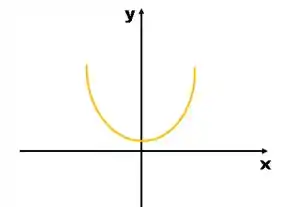
Caso 2 – Para a < 0 temos uma parábola com concavidade para baixo.

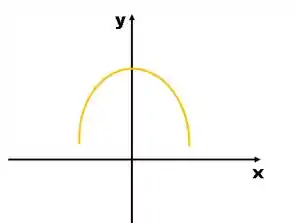
Beleza, mas por que o a não pode ser zero?

Exemplos de funções:

Para responder essa pergunta, vamos analisar a função abaixo:

f x = 2 x 2 + 3 x + 5

Temos que:

a = 2 .

b = 3 .

c = 5 .

Caso tivéssemos a = 0 , o termo x 2 sumiria e voltaríamos ao caso de uma função do primeiro grau.

f x = 0 ∙ x 2 + 3 x + 5

f x = 3 x + 5

Como montar o Gráfico de uma Função do 2º Grau?

Já vimos como definir uma função quadrática, vimos que o gráfico dessa função é uma parábola e que o sinal de a define a concavidade da parábola,

Mas como podemos realmente construir o gráfico de uma função do 2º grau?

Podemos construir o gráfico variando os valores de x e obtendo os valores respectivos em y .

Vamos construir o gráfico da função f x = x 2 + 2 x + 1

Para x = - 3 , temos:

f - 3 = ( - 3 ) 2 + 2 ∙ - 3 + 1

f - 3 = 9 - 6 + 1

f - 3 = 4

Para x = - 2 , temos:

f - 2 = ( - 2 ) 2 + 2 ∙ - 2 + 1

f - 2 = 4 - 4 + 1

f - 2 = 1

Para x = - 1 , temos:

f - 1 = ( - 1 ) 2 + 2 ∙ - 1 + 1

f - 1 = 1 - 2 + 1

f - 1 = 0

Para x = 0 , temos:

f 0 = 0 2 + 2 ∙ 0 + 1

f 0 = 1

Para x = 1 , temos:

f 1 = 1 2 + 2 ∙ 1 + 1

f 1 = 4

Esboço do gráfico

De início, como já sabemos que a > 0 , nossa parábola terá concavidade para cima.

Com os pontos que encontramos variando os valores de x , podemos montar uma tabela:

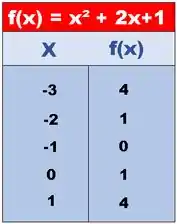
Aplicando esses pontos no gráfico teremos:

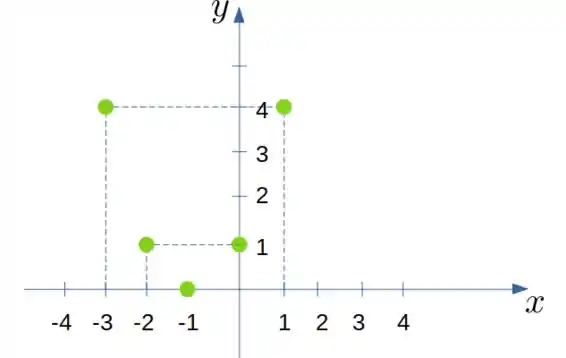
Perceba que para cada ponto no eixo y existem dois pontos no eixo x correspondente.

f - 2 = f 0 = 1

f - 3 = f 1 = 4

Esse padrão se repete infinitamente formando a parábola do gráfico.

Porém existe apenas um ponto no eixo y em que existe somente um ponto no correspondente no eixo x .

f - 1 = 0

Esse é um ponto importante da parábola, chamado de vértice.

Aguenta um pouquinho que já vamos falar dele...

Voltando ao gráfico, podemos completar seu esboço traçando uma linha curva entre os pontos que resultará na parábola.

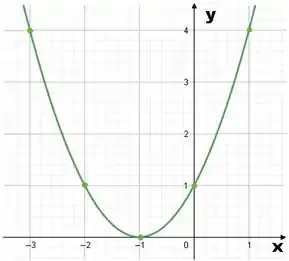
E assim conseguimos fazer um esboço do gráfico de uma função do 2º grau.

Vértice da Parábola

Já vimos o que é o vértice da parábola, mas será que existe uma fórmula para encontrar esse cara rapidamente?

É CLARO QUE EXISTE!!

Se liga...

V - b 2 a ; - ∆ 4 a

Onde,

x = - b 2 a

y = - ∆ 4 a

Se não ficou tão claro ainda, bora pra um exemplo.

Queremos encontrar o vértice da função f x = x 2 + 2 x + 1 , onde ∆ = 0 .

A coordenada do vértice é dada pelo par ordenado ( x ; y ) , para x temos:

x = - b 2 a

x = - 2 2 ∙ 1

x = - 1

Para y , temos:

y = - ∆ 4 a

y = - 0 4 ∙ 1

y = 0

Portanto, o vértice da nossa parábola se encontra na posição V - 1 ; 0 .

Exemplos de funções:

Como montar o Gráfico de uma Função do 2º Grau?

Esboço do gráfico

Vértice da Parábola

Exercícios Resolvidos

Exercício Resolvido #1

DANTE, Luiz Roberto. Tudo é matemática -9°ano.  São Paulo, SP: Ática, 2009. pp.99

Entre as sentenças abaixo indique as que representam funções quadráticas:

  1. y = x 2 - 6 x + 10
  2. y = 4 x 2
  3. y = 5 x - 7
  4. y = x 3 x - 2
  5. y = x 3 + 4 x 2 - x
  6. y = 5 x - 6 x + 4
  7. y = 5 - x 2
  8. y = x 2 + x 4 - 1
  9. y = 9 x 2 - 5 x + x - 3

Passo 1

Para resolver esse exercício, vamos lembrar a carinha de uma função quadrática.

y = a x 2 + b x + c

Onde o único coeficiente que tem que ser obrigatoriamente diferente

de 0 é o a ( a ≠ 0 ) .

Sempre o número que acompanha o x 2 é o a , que acompanha o x é o b e o número sozinho é o c .

Agora vamos analisar nossas funções

  1. y = x 2 - 6 x + 10

    2. Podemos ver que o a = 1 , b = - 6 e c = 10 . Assim, essa é exatamente uma funçãozinha do segundo grau.

  2. y = 4 x 2

    3. Nesse caso temos que a = 4 , mas não temos valores com x ou nnúmmeros sozinhos, ou seja, b = c = 0 .

    Como não temos a = 0 essa é uma função quadrática

  3. y = 5 x - 7

    4. Podemos ver que não temos x 2 na nossa equação, ou seja, a = 0 , assim não tem uma função do segundo grau.

    Passo 2

  4. y = x 3 x - 2

    5. Para descobrirmos se é uma função quadrática, temos que fazer a distributiva:

    y = x 3 x - 2

    y = 3 x 2 - 2 x

    Agora, podemos ver que a = 3 e b = - 2 . Como não temos número sozinho c = 0 .

    Assim, temos uma função quadrática.

  5. y = x 3 + 4 x 2 - x

    6. Nesse caso como temos um valor de x 3 deixou de ter uma função do segundo grau e temos uma de terceiro. Nossas funções quadráticas vão até x 2 .

  6. y = 5 x - 6 x + 4

    7. Novamente para resolver precisamos fazer à distributiva:

    y = 5 x - 6 x + 4

    y = 5 x 2 + 14 x - 24

    Agora, conseguimos ver que a = 5 , b = 14 e c = - 24 . Assim, temos uma função quadrática.

    Passo 3

  7. y = 5 - x 2

    8. Vamos dar uma ajeitadinha na nossa equação:

    y = - x 2 + 5

    Assim temos que a = - 1 e c = 5 , assim temos uma função do segundo grau.

  8. y = x 2 + x 4 - 1

    9. Quando temos uma soma no numerador de uma fração podemos abrir em duas com o mesmo denominador:

    y = x 2 4 + x 4 - 1

    Agora vemos que a = 1 4 , b = 1 4 e c = - 1 . Desta forma é uma função quadrática.

  9. y = 9 x 2 - 5 x + x - 3

Fazendo a distributiva temos: y = 9 x 2 - 44 x - 3

Onde a = 9 , b = - 44 e c = - 3

Resposta

a, b, d, f, g, h, i

Exercício Resolvido #2

DANTE, Luiz Roberto. Matemática- contexto e aplicações. ED. Renovada. São Paulo, SP: ática, 2010. pp.153

As seguintes funções são definidas sobre R . Verifique quais delas são funções quadráticas e identifique em cada uma os valores de a, b e c:

  1. f x = 2 x ( 3 x - 1 )
  2. f x = x + 2 x - 2 - 4
  3. f x = 1 + x 1 - x + x 2
  4. f x = x + 2 2 - x ( x + 1 )

Passo 1

Vamos lembrar a cara de uma função quadrática.

y = a x 2 + b x + c

Onde o obrigatoriamente a ≠ 0 .

Sempre o número que acompanha o x 2 é o a , que acompanha o x é o b e o número sozinho é o c .

Agora vamos analisar cada uma de nossas funções

  1. f x = 2 x ( 3 x - 1 )

    2. Vamos fazer à distributiva:

    f x = 6 x 2 - 2 x

    Assim temos que a = 6 , b = - 2 e c = 0 .

  2. f x = x + 2 x - 2 - 4

    3. Fazendo a distributiva:

    f x = x 2 - 8

    Onde a = 1 , b = 0 e c = - 8

    Passo 2

  3. f x = 1 + x 1 - x + x 2

    4. Abrindo, temos:

    f x = 1 - x 2 + x 2

    f x = 1

    Como a = 0 , temos que não é uma função quadrática.

  4. f x = x + 2 2 - x ( x + 1 )

Abrindo essa função:

y = x + 2 2 - x ( x + 1 )

y = x 2 + 4 x + 4 - ( x 2 + x )

y = 3 x + 4

Como a = 0 , não tem uma função do segundo grau.

Resposta

  1. a = 6 , b = - 2 e c = 0
  2. a = 1 , b = 0 e c = - 8
  3. Não é quadrática
  4. Não é quadrática

Exercício Resolvido #3

DANTE, Luiz Roberto. Tudo é matemática -9°ano.  São Paulo, SP: Ática, 2009. pp.101 (Adaptado)

Dada à função quadrática y = 3 x 2 - 4 x + 1 , determine:

  1. Os coeficientes a, b e c;
  2. y para x = 0
  3. y para x = 1
  4. y para x = - 1
  5. y para x = 1 3

Passo 1

  1. Para descobrir o valor de a, b e c, vamos lembrar que a é o coeficiente que acompanha o x 2 , b acompanha x e c é o número sozinho.

    2. Assim, olhando pra nossa funçãozinha, temos:

    y = 3 x 2 - 4 x + 1

    a = 3 , b = - 4 e c = 1

    Passo 2

  2. Nós queremos saber o valor de y quando x = 0 , vamos substituir esse valor na nossa função:

    3. y = 3 x 2 - 4 x + 1

    y = 3 0 2 - 4 ( 0 ) + 1

    y = 1

  3. Agora, queremos saber o valor de y para x = 1 , vamos substituir:

    4. y = 3 x 2 - 4 x + 1

    y = 3 1 2 - 4 ( 1 ) + 1

    y = 3 - 4 + 1 = 0

    Passo 3

  4. Agora, precisamos saber o valor de y para x = - 1 :

    5. y = 3 x 2 - 4 x + 1

    y = 3 - 1 2 - 4 ( - 1 ) + 1

    y = 3 + 4 + 1 = 8

  5. Agora, o valor de y para x = 1 3

y = 3 x 2 - 4 x + 1

y = 3 1 3 2 - 4 ( 1 3 ) + 1

y = 3 9 - 4 3 + 1

y = 1 3 - 4 3 + 1 = - 3 3 + 1

y = 0

Resposta

  1. a = 3 ,   b = - 4 e c = 1
  2. y = 1
  3. y = 0
  4. y = 8
  5. y = 0

Exercício Resolvido #4

DANTE, Luiz Roberto. Tudo é matemática -9°ano.  São Paulo, SP: Ática, 2009. pp.101 (Adaptado)

Considere a função dada por y = x 2 - 6 x + 9

  1. Essa função é quadrática?
  2. Determine os coeficientes de a,b e c para essa função
  3. Ache o valor de y para x = 0 e x = - 0,5

Passo 1

  1. Sim, ela possui todos os coeficientes a,b e c. E a ≠ 0 . Assim, temos uma função quadrática.
  2. a é o coeficiente de x 2 , assim temos que a = 1

    3. b é o coeficiente que acompanha x, nesse caso temos b = - 6

    c é o numero sozinho, c = 9

    Passo 2

  3. Para descobrir o valor, vamos substituir o valor dado de x na função.

Primeiro x = 0

y = x 2 - 6 x + 9

Substituindo: y = ( 0 ) 2 - 6 ( 0 ) + 9

y = 9

Agora para x = - 0,5 :

y = x 2 - 6 x + 9

y = ( - 0,5 ) 2 - 6 ( - 0,5 ) + 9

y = 0,25 + 3 + 9 = 12,25

Resposta

  1. Sim
  2. a = 1   ,   b = - 6 e c = 9
  3. y = 9 quando x = 0

y = 12,25 quando x = - 0,5

Exercício Resolvido #5

DANTE, Luiz Roberto. Tudo é matemática -9°ano.  São Paulo, SP: Ática, 2009. pp.92 (Adaptado)

Dada à função quadrática f x = 3 x 2 - 4 x + 1 , determine:

  1. f ( 1 )
  2. f ( 2 )
  3. f 0
  4. f ( a )
  5. f ( - 2 )

Passo 1

Para resolver esse exercício vamos usar a ideia de f ( x ) , o valor dentro dos parênteses nós vamos substituir no lugar do x na nossa função.

  1. f ( 1 ) , ou seja, vamos substituir x = 1 na nossa função:

    2. f 1 = 3 ( 1 ) 2 - 4 1 + 1 = 3 - 4 + 1

    f 1 = 0

  2. f ( 2 ) , vamos substituir x = 2 :

    3. f 2 = 3 ( 2 ) 2 - 4 2 + 1 = 12 - 8 + 1

    f 2 = 5

  3. f 0 , substituindo x = 0 :

    4. f 0 = 3 ( 0 ) 2 - 4 0 + 1 = 0 - 0 + 1

    f 0 = 1

    Passo 2

  4. f a lembrando que vamos substituir o valor dentro dos parênteses no lugar de x:

    5. f a = 3 ( a ) 2 - 4 a + 1

    f a = 3 a 2 - 4 a + 1

  5. f ( - 2 ) , ssusbtituindo

f - 2 = 3 ( - 2 ) 2 - 4 - 2 + 1 = 12 + 8 + 1

f 0 = 2 1

Resposta

  1. 0
  2. 5
  3. 1
  4. 3 a 2 - 4 a + 1
  5. 21

Exercício Resolvido #6

DANTE, Luiz Roberto. Tudo é matemática -9°ano.  São Paulo, SP: Ática, 2009. pp.103 (Adaptado)

Considere a função definida por y = 3 x 2 - 2 x - 1 para todos os valores reais de x. Responda:

  1. Essa função é afim ou quadrática?
  2. Qual a forma do seu gráfico?
  3. O Ponto ( - 1,4 ) pertence ao gráfico?
  4. Qual é o vértice da parábola?

Passo 1

  1. Se o coeficiente a fosse 0, teríamos uma função afim, mas temos a = 3 . Por isso, temos uma função quadrática.
  2. Funções do segundo grau, ou quadráticas são caracterizadas por ter gráficos em forma de parábola.

    3. Passo 2

  3. Para descobrir, vamos substituir o valor do ponto na nossa função.

    4. ( - 1,4 )

    Onde x = - 1 e y = 4

    y = 3 x 2 - 2 x - 1

    4 = 3 - 1 2 - 2 ( - 1 ) - 1

    4 = 3 + 2 - 1

    4 = 4

    Assim é um ponto pertencente ao gráfico

    Passo 3

  4. Para calcular o vértice usamos:

V - b 2 a ; - ∆ 4 a

Onde ∆ = b 2 - 4 a c

Nossos coeficientes são:

a = 3

b = - 2

c = - 1

Vamos calcular a nossa primeira posição:

- b 2 a

Substituindo os valores:

- - 2 2 3 = 2 6 = 1 3

Agora para a segunda posição temos:

- ∆ 4 a = - b 2 - 4 a c 4 a

Substituindo os valores:

- - 2 2 - 4 3 - 1 4 3 = - 4 + 12 12 = - 16 12 = - 4 3

Assim, nosso vértice é.

V 1 3 , -   4 3

Resposta

  1. Quadrática
  2. Uma parábola
  3. Sim
  4. ( 1 3 , - 4 3 )

Exercício Resolvido #7

Elaboração própria

Descubra o vértice das seguintes funções quadráticas:

  1. y = x 2  
  2. y = x 2 - 4
  3. y = - x 2 + 4 x - 2

Passo 1

Para calcular o vértice usamos:

V - b 2 a ; - ∆ 4 a

Onde ∆ = b 2 - 4 a c

  1. y = x 2

    2. Nossos coeficientes são:

    a = 1

    b = 0

    c = 0

    Vamos calcular a nossa primeira posição:

    - b 2 a

    Substituindo os valores:

    - 0 2 1 = 0

    Agora para a segunda posição temos:

    - ∆ 4 a = - b 2 - 4 a c 4 a

    Substituindo os valores:

    - 0 2 - 4 1 0 4 1 = - 0 4 = 0

    Assim, nosso vértice é.

    V 0,0

    Passo 3

  2. y = x 2 - 4

    3. Nossos coeficientes são:

    a = 1

    b = 0

    c = - 4

    Vamos calcular a nossa primeira posição:

    - b 2 a

    Substituindo os valores:

    - 0 2 1 = 0

    Agora para a segunda posição temos:

    - ∆ 4 a = - b 2 - 4 a c 4 a

    Substituindo os valores:

    - 0 2 - 4 1 - 4 4 1 = - 16 4 = - 4

    Assim, nosso vértice é.

    V 0 , - 4

  3. y = - x 2 + 4 x - 2

Nossos coeficientes são:

a = - 1

b = 4

c = - 2

Vamos calcular a nossa primeira posição:

- b 2 a

Substituindo os valores:

- 4 2 - 1 = 2

Agora para a segunda posição temos:

- ∆ 4 a = - b 2 - 4 a c 4 a

Substituindo os valores:

- 4 2 - 4 - 1 - 2 4 - 1 = - 8 - 4 = 2

Assim, nosso vértice é.

V 2,2

Resposta

  1. V 0,0
  2. V 0 , - 4
  3. V ( 2,2 )

Exercício Resolvido #8

DANTE, Luiz Roberto. Matemática- contexto e aplicações. ED. Renovada. São Paulo, SP: ática, 2010. pp.153

Gerador é um aparelho que transforma qualquer tipo de energia em energia elétrica. Se a potência Ρ (em watts) que certo gerador lança num circuito elétrico é dado pela relação Ρ i = 20 i - 5 i 2 , em que i é a intensidade da corrente elétrica que atravessa o gerador, determine o número de watts que expressa à potência Ρ quando i = 3 ampères.

Passo 1

Temos que a função da potência é:

Ρ i = 20 i - 5 i 2

E queremos saber quanto vale quando temos uma corrente de i = 3 .

Ou seja, é necessário calcular:

P ( 3 )

Passo 2

Para fazer isso, vamos pegar o valor que temos dentro dos parênteses e substituir no lugar do i, na nossa função:

Ρ 3 = 20 ( 3 ) - 5 3 2

Resolvendo, temos:

Ρ 3 = 60 - 45 = 15 w = w a t t s

Resposta

15   w a t t s