Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Conjuntos

Ver Todos os Exercícios

Teoria

E aí! Você chegou no Responde Aí! E aqui a gente te ensina tudo sobre os Conjuntos.

Pra começar, o que é um conjunto? Um conjunto nada mais é que um cara que reúne objetos (que chamaremos de elementos) que tem características comuns!

Meme Jack Chan
Meme Jack Chan

Por exemplo, se eu disse que criei um conjunto de pokémons elétricos, você logo vai pensar no pikachu, raichu, magnemite, electabuzz... e por aí vai...

A diferença é que na matemática a gente usa números, e não pokémons.

Notação de conjuntos

Vamos estabelecer algumas regras para ajudar a gente a trabalhar os conjuntos.

Quando vamos nos referir a algum conjunto, ele deverá ser chamado de uma única letra maiúscula:

O conjunto contém objetos, que são chamados de elementos do conjunto. Quando os elementos não são números, costumamos usar letras minúsculas para representar os elementos.

Por fim, você precisa saber que um conjunto é apresentado entre chaves e os elementos são separados por vírgulas!

Além disso, nós temos três formas de representar conjuntos

  1. Por extenso
  2. Por enumeração
  3. Por diagrama de Venn

Representando conjuntos por extenso

Vamos entender com um exemplo: Crie um conjunto que tenha todos os números pares positivos.

Bem simples, não é. Só tem um detalhe, existem infinitos números pares positivos! Como vamos representar então?

A primeira ideia é escrever dessa forma:

ú

Porém essa forma não costuma cair em provas. Na sua prova vai ser mais ou menos assim:

é

E a gente lê da seguinte forma:

P é um conjunto formado por x elementos, tal que cada x é um número par maior ou igual a zero

Representando conjuntos por enumeração

Para representar por enumeração, a gente simplesmente escreve alguns exemplos do conjunto entre as chaves e depois colo três pontos para indicar que o padrão continua.

Por exemplo: Crie um conjunto que tenha todos os números pares positivos.

E é só isso mesmo.

Representando conjuntos por Diagrama de Venn

O diagrama de vez é basicamente escrever os valores do conjunto dentro de um círculo oval.

Por exemplo: Crie um conjunto que tenha todos os números pares positivos.

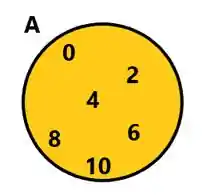
Diagrama de Venn
Diagrama de Venn

Viu?! Fácil, fácil.

Claro que estão faltando muuuuitos números, então a resposta não seria exatamente essa.

Conjuntos Finitos, Infinitos, Unitários e Vazios

Bom, essa classificação dos conjuntos é dada através da quantidade de elementos que o conjunto possui.

  1. Conjuntos Finitos: possuem quantidade finita de elementos.

    Ex: é

  2. Conjuntos Infinitos: possuem quantidade infinita de elementos.

    Ex: é

  3. Conjuntos Unitários: possuem apenas um elemento.

    Ex: é

  4. Conjuntos Vazios: não possuem elementos e são representados por ou

    Ex: é

Pertence, está contido e contém

Essa parte costuma dar um nó na nossa cabeça, mas relaxa que a partir de hoje você vai entender a diferença entre esses caras!!!

Pertence:

A gente usa esse cara quando queremos ver se um ELEMENTO pertence a um CONJUNTO.

Exemplos:

Observa esse conjunto

O valor está dentro do conjunto, então podemos dizer que: pertence a

Já o valor sozinho não está contido no conjunto pois ele esta acompanhado do valor . Então dizemos que não pertence a

Porem, a dupla existe dentro do conjunto , então dizemos que pertence a

Está Contido:

A gente usa esse cara quando queremos ver se um CONJUNTO está contido em outro CONJUNTO (se é subconjunto de um conjunto). Lembrando que um subconjunto é um conjunto cujos elementos pertencem a outro conjunto.

Por exemplo, o conjunto é um subconjunto de . Então é justo dizer que:

Por outro lado, não é um subconjunto de , pois ele é um elemento!!! Então:

Contém:

A gente usa esse cara quando queremos ver se um CONJUNTO contém um outro CONJUNTO (subconjunto).

Percebe que todos os valores de fazem parte de ? Então podemos dizer que?

OBS.: Aqui fica uma dica, o cara que está do lado das “perninhas” desse meio cursivo é quem contém o outro que está do lado da “barrigunha”. Tipo, eu nem gravo, apenas interpreto o símbolo, olha só:

Então, vamos dar uma olhada numa vídeo aula?

Viu que maneiro?! Agora da uma olhadinha aqui em baixo em uns exercícios 👇

Conjuntos Finitos, Infinitos, Unitários e Vazios

Pertence, está contido e contém

Exercícios Resolvidos

Exercício Resolvido #1

Representar, através de uma propriedade conveniente, os seguintes conjuntos:

a   A = { 0 ,   5 ,   10 ,   15 ,   20 , … }

b   B = 1 ,   2 ,   3 ,   6

Passo 1

Olááá! Anjx, o que ele quer nesse exercício é que você passe essa notação numérica para a notação por extenso! Então vamos tentar descrever cada conjunto através de palavras.

( a )

Dá uma olhada nesse conjunto:

A = 0 ,   5 ,   10 ,   15 ,   20 ,   …

Uma característica interessante é que todos os números presentes nesse conjunto são múltiplos de 5 , concorda comigo? Então seria justo escrevermos assim:

A = { x :   x   é   m ú l t i p l o   d e   5 }

Passo 2

( b )

Dá uma olhada nesse conjunto:

B = 1 ,   2 ,   3 ,   6

“Nossa, agora eu não estou vendo naaaaada de comum entre esses números!”

Relaxa, eu te ajudo! Perceba que todos eles são divisores de 6 e não negativos, concorda comigo? Então seria justo escrevermos assim:

B = { x : x   é   d i v i s o r   d e   6 }

Resposta

a   A = x : x ≥ 0   e   x   é   m ú l t i p l o   d e   5

b   B = x : x ≥ 0   e   x   é   d i v i s o r   d e   6

Exercício Resolvido #2

Representar por enumeração, os seguintes conjuntos:

a   A = x : x   é   d i v i s o r   d e   12

b   B = x : x ≥ 2   e   x   é   p a r

c   C = { x : x < 11   e   x   é   p r i m o }

Passo 1

Bora lá representar esses trens de forma numérica. O que temos que fazer aqui é verificar cada número que respeita a condição do conjunto :D

( a )

Dá uma olhada aqui:

A = { x : x   é   d i v i s o r   d e   12 }

Vamos lá, você consegue lembrar do dos divisores de 1 2 ? Se não, não tem problema. Lembre-se de que 1 é divisor de todos os números. Então, POR ENQUANTO, temos:

A = 1

Veja que 2 é divisor de 12 , o 3 também é, o 4 e o 6 também. Além disso, todo número diferente de 0 é divisor dele mesmo. Então temos:

A = { 1 ,   2 ,   3 ,   4 ,   6 ,   12 }

Passo 2

Bora fazer a letra ( b ) :

B = x : x ≥ 2   e   x   é   p a r

Cara, os números pares são aqueles que são divisíveis por 2 . Poderíamos começar pensando no 0 , mas a descrição diz que x ≥ 2 . Então nosso conjunto será:

B = { 2 ,   4 ,   6 ,   8 ,   10 ,   … }

Perceba que o conjunto é infinito, já que os números pares são infinitos.

Passo 3

Finalmente a letra ( c ) :

C = x : x < 11   e   x   é   p r i m o

Vamos começar lembrando dos primos – aquele cara que só tem o 1   e ele mesmo como seu divisor:

{ 2 ,   3 ,   5 ,   7 ,   11 ,   13 ,   17 ,   … }

Mas repara que ele pediu somente aqueles menores que 11 . Então:

C = { 2 ,   3 ,   5 ,   7 }

Resposta

a   A = 1 ,   2 ,   3 ,   4 ,   6 ,   12

b   B = 2 ,   4 ,   6 ,   8 ,   10 ,   …

c   C = { 2 ,   3 ,   5 ,   7 }

Exercício Resolvido #3

Identifique em qual formato cada conjunto abaixo está descrito e descreva-os no outro formato (por enumeração ou por extenso):

a   A = { 4 ,   9 ,   16 ,   25 }

b   B = { x : x   é   p a r   e   x   é   p r i m o }

Passo 1

a

Vamos começar com este aqui:

A = 4 ,   9 ,   16 ,   25

Aqui o conjunto foi descrito por enumeração dos elementos. Vamos passa-lo para a descrição por extenso:

Perceba que o primeiro elemento é 2 2 = 4

O segundo elemento é 3 2 = 9

O terceiro elemento é 4 2 = 16

O quarto elemento é 5 2 = 25

Então podemos escrever o seguinte:

A = x 2 : x   é   i n t e i r o   e     2 ≤ x ≤ 5  

Lendo o que escrevemos, quer dizer o seguinte: O conjunto A é formado por todos elementos x 2 tal que x é número inteiro entre 2 e 5 .

Passo 2

( b )

Nessa questão temos:

B = x : x   é   p a r   e   x   é   p r i m o

Aqui o conjunto está descrito por extenso. Então devemos descrevê-lo por enumeração. Primeiro, os números pares são:

0 ,   2 ,   4 ,   6 ,   …

Desses números, temos que pegar apenas aqueles que são primos, ou seja, que só têm o 1 e ele mesmo como divisor. Nesse caso, apenas o número 2 é primo e par. O 0 não pode ser, pois não é divisor de si mesmo.

B = 2

Resposta

a C o n j u n t o   d e s c r i t o   p o r   e n u m e r a ç ã o .   A = x 2 : x   é   i n t e i r o   e     2 ≤ x ≤ 5    

b C o n j u n t o   e s c r i t o   p o r   e x t e n s o .   B = { 2 }

Exercício Resolvido #4

Dados os conjuntos A = { 1 ,   2 ,   3 ,   4 ,   5 } e B = { a ,   b ,   c ,   d } , faça:

a A × B

( b ) B × A

Passo 1

a

Bom, aqui vamos fazer o produto cartesiano A × B , isso quer dizer que faremos pares ordenados ( e l e m e n t o   d e   A ,   e l e m e n t o   B ) seguindo a ordem dos elementos de A :

Primeiro para o 1 :

1 , a ,   1 , b , 1 , c , 1 , d

Para o 2 :

2 , a ,   2 , b , 2 , c , 2 , d

Para o 3 :

3 , a ,   3 , b , 3 , c , 3 , d

E assim sucessivamente:

A × B = { 1 , a ,   1 , b , 1 , c , 1 , d , 2 , a ,   2 , b , 2 , c , 2 , d , 3 , a ,   3 , b , 3 , c , 3 , d ,

4 , a ,   4 , b , 4 , c , 4 , d , 5 , a ,   5 , b , 5 , c , 5 , d }

Grande né? Hahaha paciência!

Passo 2

( b )

Agora vamos fazer o contrário:

B × A

Então formaremos pares ordenados do tipo ( e l e m e n t o   d e   B ,   e l e m e n t o   d e   A )

B × A = { a , 1 , a , 2 , a , 3 , a , 4 , a , 5 , b , 1 , b , 2 , b , 3 , b , 4 , b , 5 ,

c , 1 , c , 2 , c , 3 , c , 4 , c , 5 , d , 1 , d , 2 , d , 3 , d , 4 , d , 5 , }

Prontinho!

Resposta

a   A × B = { 1 , a ,   1 , b , 1 , c , 1 , d , 2 , a ,   2 , b , 2 , c , 2 , d , 3 , a ,   3 , b , 3 , c , 3 , d ,

4 , a ,   4 , b , 4 , c , 4 , d , 5 , a ,   5 , b , 5 , c , 5 , d }

( b )   B × A = { a , 1 , a , 2 , a , 3 , a , 4 , a , 5 , b , 1 , b , 2 , b , 3 , b , 4 , b , 5 ,

c , 1 , c , 2 , c , 3 , c , 4 , c , 5 , d , 1 , d , 2 , d , 3 , d , 4 , d , 5 , }

Exercício Resolvido #5

Sabendo que C = { 4 ,   9 ,   16 ,   25 ,   36 } , diga se é verdadeiro ou falso:

a   4 ∈ C

b   10 ∉ C

c   { 4 ,   36 } ⊂ C

d   9 ⊂ C

e   { 9 ,   16 } ∈ C

f   25 ∈ C

g   { 9 ,   25 } ⊄ C

Passo 1

( a )

Bora pra primeira questão!

4 ∈ C

Quando o enunciado diz isso, é a mesma coisa que falar que:

4 ∈ { 4 ,   9 ,   16 ,   25 ,   36 }

Tudo bem, estamos vendo que o elemento 4 realmente está no conjunto. Só preste atenção que quando usamos o símbolo ∈ , estamos falando sobre um ELEMENTO pertencer a um conjunto! Nessa questão, tá tudo ok. Então VERDADEIRA.

Passo 2

( b )

Seguinte, agora ele diz o seguinte:

10 ∉ C

Isso quer dizer que:

10 ∉ 4 ,   9 ,   16 ,   25 ,   36

Tudo bem, estamos vendo que o elemento 10 realmente não está no conjunto. Só preste atenção que quando usamos o símbolo ∈ , estamos falando sobre um ELEMENTO pertencer a um conjunto! Nessa questão, tá tudo ok. Então VERDADEIRA.

Passo 3

( c )

Dá uma olhada agora:

4 ,   36 ⊂ C

Traduzindo:

{ 4 ,   36 } ⊂ 4 ,   9 ,   16 ,   25 ,   36

Aqui o que ele diz é que o { 4 ,   36 } é subconjunto de 4 ,   9 ,   16 ,   25 ,   36 e isso é verdade! Tipo, o conjunto 4 ,   36 é um conjunto menorzinho que contém os mesmos elementos que estão em C , então ele é um subconjunto de C . Então VERDADEIRA.

Passo 4

( d )

Olha essa agora:

9 ⊂ C

Aqui ele está dizendo que o elemento 9 é um subconjunto de C . Isso tá estranho né? Sabe porquê? Porque quando usamos o símbolo ⊂ , estamos falando de conjuntos! E nessa questão temos um elemento. Logo, ela é FALSA.

Passo 5

( e )

Próxima letra 😊

{ 9 ,   16 } ∈ C

Bom, lendo o que está escrito: o conjunto { 9 ,   16 } pertence ao (é um elemento do) conjunto C . Isso não é verdade. Precisamos ter em mente que quando usamos o símbolo ∈ , estamos falando de elemento e veja que o conjunto não é um elemento de C .

Olha um exemplo de um conjunto que é elemento de outro:

{ 1 ,   2 ,   3 ,   4 }

Nesse caso o conjunto { 3 ,   4 } seria um elemento deste conjunto maior.

Mas esse não é o nosso caso. Então FALSA.

Passo 6

( f )

Olhemos essa agora

25 ∈ C

Isso quer dizer que 25 é um elemento do conjunto { 4 ,   9 ,   16 ,   25 ,   36 } e isso é verdade!

Então VERDADEIRA.

Passo 7

( g )

Dá uma olhada nessa última:

{ 9 ,   25 } ⊄ C

Aqui isso está dizendo que { 9,25 } não é subconjunto de C e isso não é verdade. Tipo, o conjunto 9 ,   25 é um conjunto menorzinho que contém os mesmos elementos que estão em C , então ele é um subconjunto de C . Então FALSA.

Resposta

a   V

b   V

c   V

d   F

e   F

f   V

g   F