Operações com Números Complexos
Produzido por Marcelo LuizTeoria
Motivação
Fala aí, como você está? Tudo bem?
Já bebeu água hoje? Se não, corre lá rapidinho... (Sério, me preocupo com você)
Vamos ao que interessa ...
Nesse tópico vamos aprender algumas coisas importantes no que diz respeito aos números complexos: As operações.
Já sabemos como fazer essas operações em todos os outros conjuntos só falta aprendermos a trabalhar com ela no conjunto dos números complexos.
Vamos falar nesse tópico sobre a Adição, Subtração, Multiplicação e Divisão.
Vamos nessaaaa!
Adição e Subtração
Sabemos que os números complexos sempre vão estar no formato
Onde o é a parte real e o é e a parte imaginária
A ideia é bem simples: Vamos somar e subtrair os semelhantes.
Ou seja, Parte real de um com parte real do outro e parte imaginária de um com parte imaginária do outro.
Por exemplo:
Seja
Vamos fazer
Agora basta juntar os semelhantes
O mesmo vai valer para a subtração...
Vamos trocar os sinais de quem está dentro do parênteses e depois juntar os semelhantes. Assim, ó...
Show?
Multiplicação e Divisão
Vamos a nossa multiplicação...
De cara você vai perceber que usaremos coisas que (muito provavelmente) já vimos antes.
Seja
Fazendo a multiplicação, teremos
Agora basta fazermos a distributiva
Até aí, ok?
Só não esquece do seguinte...
Portanto...
Juntando os semelhantes, temos
Na multiplicação, temos um fato interessante. Toda vez que multiplicamos um número complexo pelo seu conjugado (mesmo número, mas com a parte imaginária tendo sinal trocado), encontramos um número real. Por exemplo:
Lembra dessa ideia porque vamos usá-la em breve, tá?
Agora vamos a divisão, utilizaremos os mesmos números complexos do exemplo anterior. Teremos o seguinte...
Agora, a pergunta que não quer calar é...
COMO VAMOS RESOLVER ISSO?
Se você pensou em “dividir os semelhantes”...
Daí teremos
Certo?
.
.
.
.
Parabéns, você acabou de ERRAR hahahaha

Não podemos fazer isso, porque sempre precisamos pensar na divisão como o inverso da multiplicação. Por exemplo
No entanto, se fizéssemos
Se multiplicássemos
Teríamos
Ok, já deu pra perceber que o resultado disso será BEEEEM diferente de
Como resolveremos isso então?
Na verdade, vamos utilizar uma outra ideia...
Se multiplicarmos uma fração, por uma outra que tenha os mesmos valores no numerador e no denominador, manteremos a nossa fração inicial. Por exemplo:
Mas por que isso é importante?
Porque poderemos reescrever a nossa divisão transformando o nosso denominador em um número real... Mas como faremos isso?
Usando o CONJUGADO do denominador.
Da seguinte forma...
É isso que vamos fazer toda vez que quisermos fazer uma divisão... Vamos achar o conjugado do nosso denominador e depois vamos multiplicar o numerador e o denominador por ele. Tranquilo, né?
Potências de
Pra fecharmos esse nosso papo, vamos falar sobre o nosso amigão imaginário, isso mesmo... O nosso “”. Já sabemos que ...
Mas quanto vale ou?
Difícil saber?
Calma, vamos pensar nisso um pouco mais devagar
E assim por diante...
Você deve ter percebido que sempre teremos os mesmos valores aparecendo, mas pra facilitar o nosso trabalho, vamos pensar no seguinte: Pelo cálculo que fizemos , ou seja, sempre vai compensar colocar nosso expoente em função do 4, como assim?
Vamos calcular aquelas potências que vimos no início...
Primeira coisa que vamos fazer é dividir o é o nosso expoente por . Fica assim, ó...
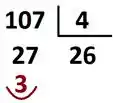
Ou seja, podemos escrever o como
Sendo assim,
De modo geral, basta você dividir o expoente por 4 e o valor que você encontrar no resto, será o novo expoente.
Show?
Agora #PartiuExercicios