Binômio de Newton
Teoria
Introdução
FAAAAAALA AÍ, MESTRE DOS POLINÔMIOS! Hahahaha Cara, eu encho muito a sua bola!
Seguinte, vou começar te mostrando a motivação dessa teoria. Já estamos cansados de ver potências do tipo:
“Af, Paula! Já estou exaustx de ver isso, sei de cor!”
Eu sei, meu anjo. Porém, suponha que eu te peça para desenvolver essa potência:
Eita, agora complicou né?
Para isto temos o nosso Binômio de Newton, para nos ajudar a expandir potências dessa forma:
Números Binomiais
Antes de eu te dar aquela fórmula marota, bora ter uma noção do que é um número binomial (bonito, né? Me acho quando falo isso hahaha).
É o seguinte, este termo está muito ligado à combinatória, que é um assunto futuro! Embora você ainda não tenha aprendido, já deve ter ouvido falar em “ escolhe ”. Essa frase é matematicamente representada desse jeito:
Onde e :
Onde
Se liga, que usaremos isso daqui a pouco!
Termo Geral
Primeiramente, quero te mostrar novamente os seguintes produtos notáveis:
Perceba que a nossa potência é e a quantidade de termos é . E ainda:
Note que a potência é e a quantidade de termos é .
Portanto, podemos notar que quando temos uma potência da forma , teremos termos. Legal, só queria que você visse essa observação, não só engolisse.
Não entrarei em detalhes, mas
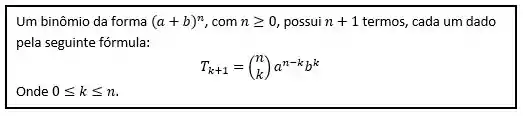
Olha só! Apareceu nosso número binomial!
Bom, essa fórmula serve para ... E se você se deparar com ?
“Eu choro!”
Bobx você! Repare que:
Bora substituir isso na fórmula:
Pronto, chegamos na fórmula! Perceba que tem não problema você esquecer a próxima, é só pensar desse jeitinho!
Triângulo de Pascal
ANJOOO, já te adianto que esse subtítulo é apenas para ajudar você! Não precisa se matar para se dar bem com isso, afinal, você não é obrigado a usar o Triângulo de Pascal.
“Para que usamos?”
Bom, a gente usa para pegar os coeficientes das nossas potências. Vamos construí-lo e daí eu te mostro exemplos.
Eu particularmente gosto muito dele, a gente constrói da seguinte forma. Primeiro, você começa com o número :
Essa é a primeira linha. Lembre-se: a linha tem termos.
Essa linha tem o coeficiente de
Vamos para a segunda linha, sabendo que o primeiro e o último termo de cada linha são o número :
Essa última linha que construímos tem os coeficientes de
E agora, a gente constrói os termos! Dessa forma:
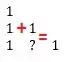
Então:
Essa última linha que construímos agora tem os coeficientes de
Bom, já temos linhas, olha a quarta:
Adivinha só? A última linha tem os coeficientes de
Perceba que:
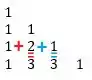
Como deveria ser! Olha a quinta linha:
Esta possui os coeficientes de
E a sexta:
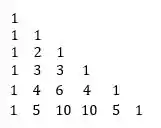
Esta possui os coeficientes de
Você pode sair fazendo quantas linhas você precisar!
Soma dos Coeficientes
Vamos supor que te pedem o seguinte numa questão:
Você pode expandir isso pela fórmula, pode usar o Triângulo de Pascal também, mas eu vou te dar uma dica que vai te ajudar muito nesse tipo de questão: basta chamar esse binômio de e calcular .
“De onde você tirou isso?”
Se liga, você já é mestre dos polinômios, então vou colocar aqui embaixo a forma geral de um polinômio:
Se substituímos :
Olha que lindo, temos justamente a soma dos coeficientes!!! Então, fica a dica!
No nosso caso:
Então a soma dos coeficientes é .
Termo Geral
Triângulo de Pascal
Soma dos Coeficientes
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Desenvolver as potências abaixo:
Passo 1
FAAAALA AÍ, meu anjo! Tudo bom? Vamos finalmente colocar a mão na massa! Começando do começo:
Bom, vou fazer esse item de duas formas: usando a fórmula geral e usando o Triângulo de Pascal (jeito que eu faço). Aí você vê com qual você se identifica mais.
forma (jeito que eu faço):
Um binômio da forma tem termos.
No nosso caso, . Eu gosto de fazer da seguinte forma: como eu sei que tem termos, eu começo assim:
Pronto, tenho cinco termos. Agora eu preencho todas as potências de , já que ele vem primeiro no binômio. As potências começam no expoente máximo, que é e vão até o :
Agora eu preencho o expoente de , a ideia é a seguinte: o expoente é o número que falta para a soma dos expoentes chegarem a . Por exemplo, no primeiro termo temos o expoente , para chegar a falta , então:
Perceba que se somarmos o expoente dos dois, a soma dá ,e então está tudo certinho!
Passo 2
Só faltam os coeficientes! E como temos termos, é tranquilo olhar no Triângulo Pascal a quinta linha!
“Ah, mas eu não sei como é o Triângulo de Pascal!”
Vou te ensinar a construir. Primeiro, você começa com o número :
Essa é a primeira linha. Lembre-se: a linha tem termos.
Vamos para a segunda linha, sabendo que o primeiro e o último termo de cada linha são o número :
E agora, a gente constrói os termos! Dessa forma:
Então:
Bom, já temos linhas, olha a quarta:
Perceba que:
Como deveria ser! Finalmente, a quinta linha:
Passo 3
Prontinho! Vamos substituir:
E agora é só ajeitar as potências, sabendo que :
Esse método não costuma ser longo, eu só quis esmiuçar bem para você entender o raciocínio!
Passo 4
forma (fórmula):
Sabendo que o um binômio da forma tem termos, a fórmula do termo geral é
No nosso caso, e . Então vamos calcular termo a termo (lembrando que temos ):
Então, temos os seguintes termos:
Passo 5
Agora vamos resolver os números binomiais:
Começando:
Lembrando que .
Passo 6
Pronto! Agora substituímos:
Finalmente:
Finalizando:
Passo 7
Bom, vou fazer esse item de duas formas: usando a fórmula geral e usando o Triângulo de Pascal (jeito que eu faço). Aí você vê com qual você se identifica mais.
forma (jeito que eu faço):
Um binômio da forma tem termos.
“Mas aqui nós temos um , não um ”
Eu sei, mas olha só o que podemos fazer:
No nosso caso, . Eu gosto de fazer da seguinte forma: como eu sei que tem termos, eu começo assim:
Pronto, temos seis termos. Agora eu preencho todas as potências de , já que ele vem primeiro no binômio. As potências começam no expoente máximo, que é e vão até o :
Agora eu preencho o expoente de , a ideia é a seguinte: o expoente é o número que falta para a soma dos expoentes chegarem a . Por exemplo, no primeiro termo temos o expoente , para chegar a falta , então:
Perceba que se somarmos o expoente dos dois, a soma dá ,e então está tudo certinho!
Passo 8
Só faltam os coeficientes! E como temos termos, vamos olhar no Triângulo Pascal a sexta linha!
“Ah, mas eu não sei como é o Triângulo de Pascal!”
Bom, já construímos até a linha :
Vamos fazer a linha :
Passo 9
Prontinho! Vamos substituir:
E agora é só ajeitar as potências, sabendo que e :
Passo 10
forma (fórmula):
Sabendo que o um binômio da forma tem termos, a fórmula do termo geral é
No nosso caso, e . Então vamos calcular termo a termo (lembrando que temos ):
Então, temos os seguintes termos:
Passo 11
Agora vamos resolver os números binomiais:
Começando:
Lembrando que .
Passo 12
Pronto! Agora substituímos:
Finalmente:
Finalizando:
Resposta
Exercício Resolvido #2
Elaboração Própria
Desenvolvendo-se o binômio , podemos dizer que a soma de seus coeficientes é:
Passo 1
Olááá, queridx alunx! Tudo bom?
Nesse exercício, nós precisamos saber a soma dos coeficientes daquele binômio. Podemos descobrir de três formas: calculando , usando o Triângulo de Pascal ou desenvolvendo o binômio.
forma (calculando ):
Sabemos que dado um polinômio , a soma dos coeficientes é :
Bem rápido, né?!
forma (Triângulo de Pascal):
Um binômio da forma tem termos.
No nosso caso, . Eu gosto de fazer da seguinte forma: como eu sei que tem termos, eu começo assim:
Mas como elevado a qualquer coisa é :
Pronto, tenho seis termos. Agora eu preencho todas as potências de , já que ele vem primeiro no binômio. As potências começam no expoente máximo, que é e vão até o :
Cara, perceba que os coeficientes vão ser justamente os caras da linha no Triângulo de Pascal.
Passo 2
Só faltam os coeficientes! E como temos termos, é tranquilo olhar no Triângulo Pascal a sexta linha!
“Ah, mas eu não sei como é o Triângulo de Pascal!”
Vou te ensinar a construir. Primeiro, você começa com o número :
Essa é a primeira linha. Lembre-se: a linha tem termos.
Vamos para a segunda linha, sabendo que o primeiro e o último termo de cada linha é o número :
E agora, a gente constrói os termos! Dessa forma:
Então:
Bom, já temos linhas, olha a quarta:
Perceba que:
Como deveria ser! A quinta linha:
Finalmente, a sexta linha:
Pronto! Esses termos da linha são os nossos coeficientes. E como queremos a soma, basta soma-los:
Passo 3
forma (fórmula):
Sabendo que o um binômio da forma tem termos, a fórmula do termo geral é
No nosso caso, e . Então vamos calcular termo a termo (lembrando que temos ):
Então, temos os seguintes termos:
Então a expansão é:
Como queremos a soma dos coeficientes, temos que somar esses números binomiais!
Passo 4
Agora vamos resolver os números binomiais:
Começando:
Lembrando que .
Passo 5
Pronto! Agora substituímos:
E a soma desses termos é .
Resposta
Exercício Resolvido #3
Elaboração Própria
Qual o termo no desenvolvimento da potência ?
Passo 1
Bom, nessa questão teremos que usar a fórmula do termo geral para potências do tipo , onde temos termos:
No nosso caso e .
Portanto, se queremos o termo , precisamos que:
Então é só substituirmos por na fórmula:
Passo 2
Agora vamos resolver o número binomial:
Começando:
Passo 3
Substituindo:
Resposta
Exercício Resolvido #4
Elaboração Própria
Dado o binômio abaixo, determine o coeficiente que acompanha o termo :
Passo 1
Faaaaala aí, meu anjo! Para esse tipo de questão, teremos que usar a fórmula do termo geral.
Dada uma potência da forma , se desenvolvermos teremos termos, cuja fórmula geral é:
Onde no nosso caso e .
Substituindo essas informações na fórmula:
Finalmente:
Passo 2
Como nós queremos o coeficiente que acompanha , precisamos encontrar algo do tipo:
Então temos:
Vamos substituir o para encontrarmos, enfim, o termo:
Passo 3
Lembrando que:
Portanto:
Logo, o coeficiente que acompanha é .
Resposta
Exercício Resolvido #5
Elaboração Própria
Determine o coeficiente que acompanha o termo no desenvolvimento da potência .
Passo 1
Faaaaala aí, meu anjo! Para esse tipo de questão, teremos que usar a fórmula do termo geral.
Dada uma potência da forma , se desenvolvermos teremos termos, cuja fórmula geral é:
Onde no nosso caso e .
Substituindo essas informações na fórmula:
Finalmente:
Passo 2
Como nós queremos o coeficiente que acompanha , precisamos encontrar algo do tipo:
Então temos:
Vamos substituir o para encontrarmos, enfim, o termo:
Passo 3
Lembrando que:
Portanto:
Logo, o coeficiente que acompanha é .
Resposta
Exercício Resolvido #6
Elaboração Própria
Determine o valor de para que as seguintes igualdades sejam verdadeiras.
Passo 1
Bom, nessa questão precisamos lembrar da seguinte relação:
Onde .
Vamos começar pelo começo:
A única forma de isso ser verdade é:
- Se e forem iguais.
- Se a soma dos termos e for , ou seja, se um for complementar do outro em relação a .
- Se e forem iguais.
- Se a soma dos termos e for , ou seja, se um for complementar do outro em relação a .
Isto é, ou .
Passo 2
A única forma de isso ser verdade é:
Mas isso não é possível porque teríamos um caso de , , logo, isso não obedece à condição.
Isto é, .