Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Círculo Trigonométrico

Ver Todos os Exercícios

Teoria

Fala aí! Bora aprender como usar o Círculo Trigonométrico de uma vez por todas?!

Então se liga nesse vídeo super completo que a gente preparou especialmente pra você! 👇 🧡

Ou então segue comigo num resumo em texto! 👇

O que é um Círculo Trigonométrico e pra que serve?

O círculo trigonométrico é um círculo de raio , com uma circunferência centrada em e ele é muuuito importante dentro da trigonometria!

Ele tem essa carinha aqui:

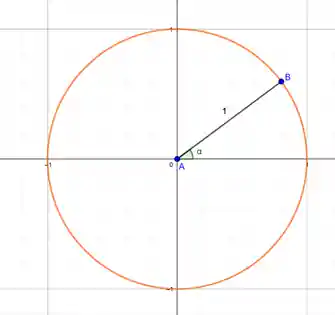
Círculo trigonométrico.
Círculo trigonométrico.

Com ele podemos escrever as relações trigonométricas para QUALQUER ângulo!

Quadrantes

O círculo trigonométrico é dividido em quadrantes iguais de ou .

Assim:

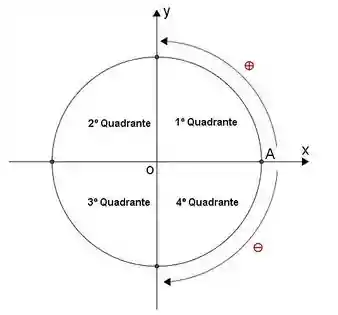
Círculo trigonométrico: Quadrantes
Círculo trigonométrico: Quadrantes

Dentro do círculo, consideramos o ângulo de análise partindo da parte positiva do eixo  e crescendo no sentido anti-horário, como podemos observar na figura acima. Quando giramos no sentido horário, acrescentamos um sinal negativo na frente do ângulo!

Razões Trigonométricas

Sabe aquele valor que aparece na calculadora quando você quer o seno, cosseno ou tangente de algum ângulo? Esses valores saem no círculo trigonométrico!

Quer descobrir como? Então se liga na imagem abaixo:

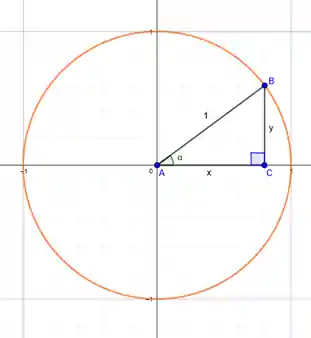
Relações trigonométricas
Relações trigonométricas

O seno é o eixo do círculo trigonométrico e o cosseno é seu eixo e eu vou te provar! Pra isso vamos usar as fórmulas de seno e cosseno que já conhecemos:

Viu!? Agora tangente:

É claro que existem outras relações trigonométricas, mas essas são as mais importantes!

Sinais das Razões Trigonométricas

No circulo trigonométrico estamos lidando com eixos, como vimos ali em cima, o seno fica no eixo e o cosseno no eixo , então pra saber se o seno ou cosseno de um ângulo é positivo ou negativo, tudo o que você precisa fazer é se ligar em qual quadrante seu ângulo esta!

A imagem abaixo dá uma resumida nos sinais, mas não precisa decorar, é só lembrar da posição do ângulo:

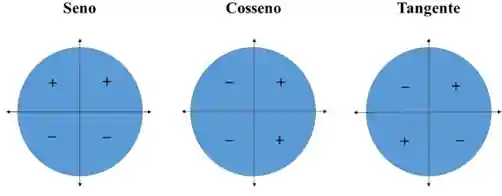
Sinais das razões trigonométricas nos quadrantes do círculo trigonométrico.
Sinais das razões trigonométricas nos quadrantes do círculo trigonométrico.

Como a tangente é a razão entre o seno e cosseno, é só avaliar os sinais e sucesso!

Grau ou Radiano?

A gente pode representar um ângulo usando a unidade de grau ou radiano, então é muito importante sabermos converter essas unidades!

Uma volta completa no círculo trigonométrico corresponde a ou , a forma mais simples de converter uma unidade em outra é com a boa e velha regra de três!

Ou então vc pode fazer:

Ângulos Notáveis

Os ângulos notáveis são ângulos mais conhecidos e mais cobrados na prova! Por isso vale a pena decorar eles, se liga nessa tabelinha:

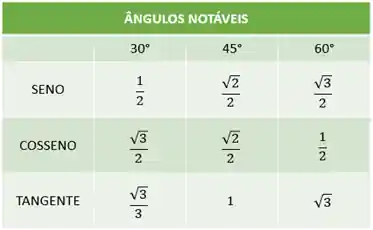
Ângulos Notáveis
Ângulos Notáveis

Agora dá só uma olhada nos ângulos notáveis no círculo trigonométrico:

Ângulos notáveis no círculo trigonométrico.
Ângulos notáveis no círculo trigonométrico.

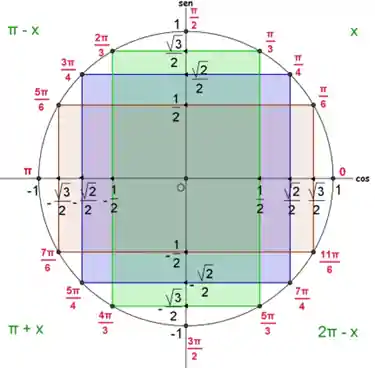
Podemos perceber que é igual ao e ambos são iguais a e . O mesmo raciocínio pode ser feito com qualquer ângulo do círculo trigonométrico!

Ângulos Congruentes

A partir do círculo trigonométrico, vemos que a cada , ou , damos uma volta completa e os valores de seno e cosseno se repetem. Chamamos os ângulos com relações trigonométricas em comum de ângulos congruentes.

Por exemplo, é congruente de , pois:

Logo, teremos:

De maneira geral, podemos dizer que:

Com . precisa ser um número inteiro, pois somente dando uma volta inteira, voltamos ao mesmo lugar.


Agora, vamos praticar com exercícios?!

Quadrantes

Grau ou Radiano?

Ângulos Notáveis

Ângulos Congruentes

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

60 ° (graus) em radianos equivale a

  1. π 3
  2. π 6
  3. π 4
  4. 3 π 2

Passo 1

Fala Aíí!! Para resolver essa questão vamos partir do fato de que uma volta completa no círculo trigonométrico corresponde, em graus, a 360 ° e, em radianos, 2 π .

Tá... mas como conseguimos transformar 60 ° em radiano??

Conseguimos fazer isso através de uma regra de 3 simples!!! Vamos ver como vai funcionar agora!!

Passo 2

Para encontrar o valor de 60 ° em radianos utilizaremos a regra de 3 simples abaixo

Multiplicando cruzado, temos

360 x = 2 π ∙ 60

360 x = 120 π

Isolando o x , ficamos com

x = 120 π 360

Simplificando, temos

x = π 3

Ou seja, 60 ° em radianos vale π 3 !

Belezinha?!

Resposta

Letra A

Exercício Resolvido #2

Elaboração Própria

2 π 3   radianos em graus equivale a:

  1. 270 °
  2. 120 °
  3. 110 °
  4. 130 °

Passo 1

Fala Aííí!! Nessa questão temos o ângulo 2 π 3 em radianos e queremos transformá-lo em graus, certo? Como podemos fazer isso??

Para resolver essa questão, precisamos lembrar que

π = 180 °

Beleza?!

Passo 2

Para encontrarmos o valor do ângulo em graus, basta substituir o valor de π por 180 ° !! Assim,

2 π 3

2 180 3

Fazendo as continhas, temos

360 3 = 120 °

Ou seja, 2 π 3 equivale a 120 ° !

Show de bola?!

Resposta

Letra B

Exercício Resolvido #3

Elaboração Própria

Transforme 140 ° (graus) em radianos.

Passo 1

Vamos láá!! Para resolver essa questão vamos partir do fato de que uma volta completa no círculo trigonométrico corresponde, em graus, a 360 ° e, em radianos, 2 π .

Tá... mas como conseguimos transformar 14 0 ° em radianos?? Conseguimos fazer isso através de uma regra de 3 simples!!! Vamos ver como vai funcionar agora!!

Passo 2

Para encontrar o valor de 14 0 ° em radianos utilizaremos a regra de 3 simples abaixo

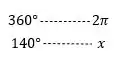
Multiplicando cruzado, temos

360 x = 2 π ∙ 14 0

360 x = 28 0 π

Isolando o x , ficamos com

x = 280 π 360

Simplificando, temos

x = 7 π 9

Ou seja, 14 0 ° em radianos vale 7 π 9 !

Belezinha?!

Resposta

7 π 9

Exercício Resolvido #4

Elaboração Própria

Transforme π 18 radianos em graus.

Passo 1

Nessa questão temos o ângulo π 18 em radianos e queremos transformá-lo em graus, certo? Como podemos fazer isso??

Para resolver essa questão, precisamos lembrar que

π = 180 °

Show de bola?!

Passo 2

Para encontrarmos o valor do ângulo em graus, basta substituir o valor de π por 180 ° !! Assim,

π 18

Substituindo, temos

180 18

Fazendo as continhas, temos

180 18 = 10 °

Ou seja, π 18 equivale a 1 0 ° !

Show de bola?!

Resposta

10 °

Exercício Resolvido #5

Elaboração Própria

Quanto vale o s e n o ( 120 ° ) ?

  1. 2 2
  2. 3 2
  3. 2 3 3
  4. 1

Passo 1

Fala Aííí!! Como podemos calcular o s e n o de um ângulo que não está no primeiro quadrante??

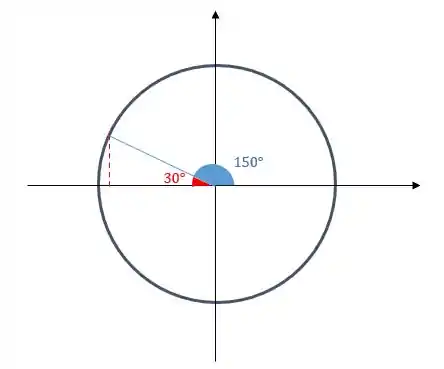
Calma que vamos ver que calcular o s e n o desses valores não é difícil!! Basta a gente observar a simetria do círculo trigonométrico. Primeiro vamos olhar para o ângulo de 120 ° no círculo trigonométrico:

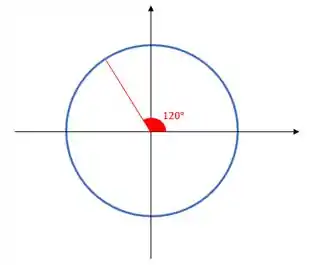
Note que esse ângulo de 120 ° , para chegar a 180 ° , está faltando 60 ° , beleza?!

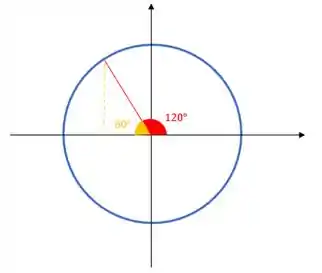
Show de bola?!

Passo 2

Como o ângulo de 60 ° está no segundo quadrante, repare que o s e n o que é sempre dado no eixo y é positivo... (Uma dica é lembrar que o s e n o está sem sono, então ele está de pé rs)

Assim,

s e n o 120 ° = s e n o 60 °

Se olharmos para a nossa tabelinha dos ângulos notáveis, podemos encontrar o valor de s e n 60 °

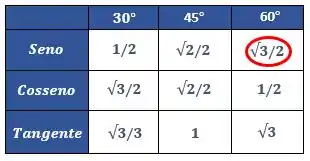
Ou seja,

s e n o 120 ° = s e n o 60 ° = 3 2

Show de bola?!

Resposta

L e t r a   B

Exercício Resolvido #6

Elaboração Própria

Quanto vale o c o s s e n o ( 135 ° ) ?

  1. - 2 2
  2. 3 2
  3. - 2 3 3
  4. 1

Passo 1

Vamos láá!! Como podemos calcular o s e n o de um ângulo que não está no primeiro quadrante??

Calma meu pupilo!!! Vamos ver que calcular o c o s s e n o desses valores não é difícil!! Basta a gente observar a simetria do círculo trigonométrico. Primeiro vamos olhar para o ângulo de 135 ° no círculo trigonométrico:

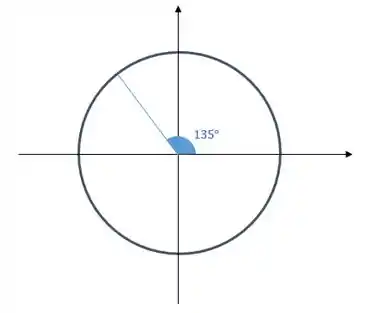
Note que esse ângulo de 135 ° , para chegar a 180 ° , está faltando 45 ° , beleza?!

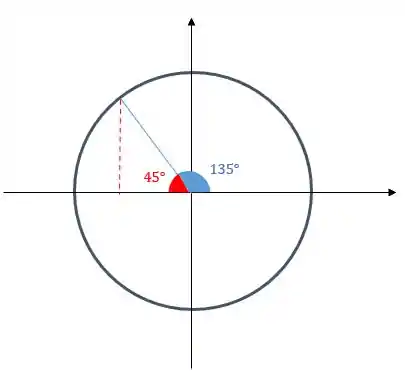
Show de bola?!

Passo 2

Como o ângulo de 45 ° está no segundo quadrante, repare que o c o s s e n o que é sempre dado no eixo x é negativo... (Uma dica é lembrar que o c o s s e n o está com sono, então ele está de pé rs)

Assim,

c o s s e n o 135 ° = - c o s s e n o 45 °

Se olharmos para a nossa tabelinha dos ângulos notáveis, podemos encontrar o valor de c o s s e n 45 °

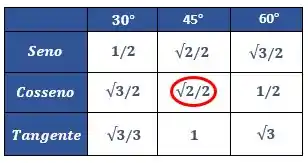
Ou seja,

c o s s e n o 135 ° = - c o s s e n o 45 ° = - 2 2

Show de bola?!

Resposta

L e t r a   A

Exercício Resolvido #7

Elaboração Própria

Quanto vale o s e n o ( 150 ° ) ?

  1. 2 2
  2. 3 2
  3. 2 3 3
  4. 1 2

Passo 1

Vamos láá!! Como podemos calcular o s e n o ( 150 ° ) ??

Basta a gente observar a simetria do círculo trigonométrico. Primeiro vamos olhar para o ângulo de 1 50 ° no círculo trigonométrico:

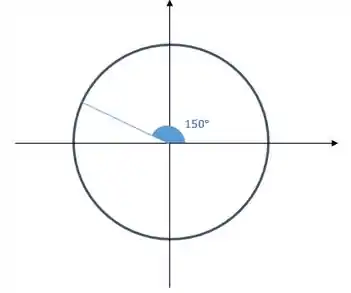
Note que esse ângulo de 150 ° , para chegar a 180 ° , está faltando 30 ° , beleza?!

Show de bola?!

Passo 2

Como o ângulo de 30 ° está no segundo quadrante, repare que o s e n o que é sempre dado no eixo y é positivo... (Uma dica é lembrar que o s e n o está sem sono, então ele está de pé rs)

Assim,

s e n o 1 5 0 ° = s e n o 30 °

Se olharmos para a nossa tabelinha dos ângulos notáveis, podemos encontrar o valor de s e n 30 °

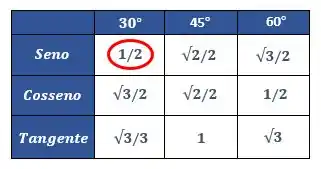
Ou seja,

s e n o 15 0 ° = s e n o 30 ° = 1 2

Show de bola?!

Resposta

L e t r a   D

Exercício Resolvido #8

Elaboração Própria

Em qual quadrante está localizado o ângulo de 600 ° ?

  1. 1 º Quadrante
  2. 2 º Quadrante
  3. 3 º Quadrante
  4. 4 º Quadrante

Passo 1

Fala Aíí!! Como podemos encontrar em qual quadrante está localizado o ângulo de 600 ° ???

Calma meu pequeno gafanhoto!!! Veremos aqui que é mais simples do que você imagina!!!

Pensa comigo: Uma volta completa no círculo trigonométrico equivale a 360 ° , concorda?! O que vamos fazer aqui então é dividir 600 ° por 360 ° , para saber quantas voltas daremos no círculo trigonométrico... maaaaas, isso não é o mais importante!

O que vai nos interessar aqui é o resto da divisão!!! Ele indicará o valor do ângulo correspondente ao quadrante! Vamos ver como funciona na prática????

Passo 2

Dividindo 600 ° por 360 ° temos

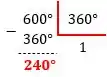
Opaaa! Se você reparar o resto da nossa divisão deu 240 ° . Isso significa que o nosso ângulo deu uma volta completa e terminou no ponto do círculo correspondente ao ângulo de 240 ° .

Agora pra fechar com chave de ouro, sabemos que o ângulo de 240 ° está no 3 ° quadrante, certo?!

Portanto, o ângulo de 600 ° está no 3 º quadrante.

Resposta

L e t r a   C

Exercício Resolvido #9

UVA - Fernando Marinho - Lista 3 - 1b

Calcule a primeira determinação positiva do conjunto de arcos de mesma extremidade que o arco A de medida: A = - 2000 º

Passo 1

Eu não sei você, mas achei esse meio confuso!

Bom...Basicamente nós queremos achar um arco positivo que seja congruente a esse arco A do enunciado, ou seja, queremos um arco positivo que “chegue no mesmo ponto” do que o arco A . Para tal, temos que adicionar 360 k (ou seja, k voltas) e ver o menor valor de k que leva a um ângulo positivo. Vamos lá: - 2000 º + 360 k > 0

Onde k é um número inteiro!

Passo 2

Pô...vamos fazer o seguinte: vamos ver qual seria o número de voltas k que deveríamos dar para chegarmos no arco de ângulo 0 ° . Portanto,

360 k > 2000 → k > 5,55555 …

O valor de k deu 5,555 … , né? Então, galera, como k representa o número de voltas, ele tem que ser um número inteiro. Deste modo, o menor valor de k maior que 5,555 . . . é k = 6 .

Passo 3

Agora vamos substituir os candidatos e ver o que achamos. Para k = 6 :

- 2000 º + 360   ⋅ 6 = 160 °

Dessa maneira, k = 6 garante o menor ângulo positivo = 160 ° .

Resposta

160 o

Exercício Resolvido #10

UVA - Fernando Marinho - Lista 3 - 4b

Determine o valor de:

cos ⁡ 3555 º

Passo 1

Vamos achar o arco congruente desse ângulo na primeira volta para podermos calcular. Na verdade a gente quer escrever esse ângulo como um múltiplo de 360 o , ou seja, 360 k somado a um ângulo em um dos quatro quadrantes, α . Portanto, 3555 = 360 k + α

Passo 2

O que precisamos definir é o α ! Mas, isso é mole, pois esse valor é exatamente o resto da divisão de 3555 por 360!

Fazendo as contas, nós temos que o quociente da divisão vale 9 e o resto é 315! Ou seja, 3555 é o mesmo arco que começar em 315 e dar 9 voltas!

Passo 3

Mas ainda não está legal: cos ⁡ 315 º

Você sabe o valor? É, é meio chato ver isso de cara. Mas repare que 315 º está há 45 º de 360 º que está na origem, então é equivalente a: cos ⁡ - 45 º

Pois se saíssemos da origem no sentido anti-horário e percorrêssemos 45 º chegaríamos no mesmo ponto que está no 4º quadrante

Pelo círculo trigonométrico, uma vez que o cosseno é o eixo x , os seus valores tem o mesmo sinal no primeiro e quarto quadrantes (enquanto que o seno tem sinais iguais no primeiro e segundo quadrantes e terceiro e quarto). Assim:

cos ⁡ 3555 º = cos ⁡ 315 º = cos ⁡ - 45 º = 2 2  

Resposta

cos ⁡ 3555 º = 2 2

Exercício Resolvido #11

UVA - Fernando Marinho - Lista 3 - 4c

Determine o valor de: tg ⁡ - 35 π 4

Passo 1

Novamente, temos que achar um ângulo congruente mais adequado. Para tal, vamos determinar o menor valor de k para que o ângulo esteja na primeira volta: - 35 π 4 + 2 π k = - 35 π 4 + 8 π k 4 = 8 π k - 35 π 4

Testando para k = 5 :

8 π k - 35 π 4 = 8 π ⋅ 5 - 35 π 4 = 40 π - 35 π 4 = 5 π 4

Como a tangente se repete a cada π rad, podemos melhorara ainda mais isso, reduzindo π rad:

5 π 4 - π = π 4

Que é 45 º . Agora tá na tabelinha. Ficou fácil:

tg ⁡ - 35 π 4 = tg ⁡ 5 π 4 = tg ⁡ π 4 = 1

Resposta

tg ⁡ - 35 π 4 = 1

Exercícios de Livros Relacionados

Calcule o valor da expressão s e n 105 ° - c o s 75 ° .
Calcule cotg 165°, sec 255° e cossec 15°.
Sejam α = a r cs e n 4 5 um arco no 2º quadrante e β = a r ct g - 4 3 um arco no 4º quadrante. Calcule 25 c o s ⁡ ( α + β ) .
Determine os seguintes números: a r c t g 0 , a r c t g sqrt(3) , a r c t g (- 1) , a r c t g ((- sqrt(3))/(3)) .
Calcule:a ) s e n (a r c t g 2 + a r c t g 3) . b ) cos (a r c t g 2 - a r c t g (1)/(2)) . c ) t g (2 a r c t g (1)/(5)) . d ) cos (3 a r c t g (24)/(7)) .