Equações de Graus Maiores
Teoria
Para equações do 1º e 2º grau temos um caminho bem definido de como chegar nas soluções, mas por aqui as coisas complicam um pouquinho na hora de resolver as equações de grau maior que 2.
Até existe uma fórmula que pode ser usada pra resolver equações do 3º grau, por exemplo, mas ela é bem complicada e já não vale a pena a gente tentar usá-la.
Mas não se desespere! Vamos aproveitar as soluções fáceis pra lidar com problemas difíceis!
Na prática, quando encontrar uma equação de grau maior que 2, vamos dar um jeito de transformar a equação para que tenhamos uma de grau menor e fique mais fácil resolver.
Aqui, vamos aprender dois jeitos de fazer isso. Vem comigo!
Fatoração
É bem fácil saber quando podemos usar esse método, sempre que a nossa equação tiver em todos os termos. Por exemplo:
O que vamos fazer então é colocar o em evidência! Vamos colocar a expressão entre parênteses, com o comum de todos os termos do lado de fora, pra isso, vamos dividir cada termo da equação por :
Agora, podemos observar duas coisas importantes! A primeira é que, como temos um sozinho do lado de fora, se , toda a expressão será zerada independente do valor que tivermos dentro do parêntese. Isso significa que é uma das soluções da nossa equação!
A segunda observação importante é que o que sobrou dentro dos parênteses é uma expressão do 2 grau, que podemos resolver com a fórmula de Bhaskara!
Encontramos então as três soluções da nossa equação: , e !
Um detalhe importante é que o número de soluções sempre será igual ao grau que tivermos, como aqui que a equação era de grau , encontramos soluções!
Briot-Ruffini
Suponha agora que você se depare com isso:
Vou começar revelando o ponto fraco desse método, pra usá-lo precisamos conhecer pelo menos uma raiz da expressão que queremos reduzir o grau. Nesse caso, vamos testar alguns valores de e ver se damos sorte:
Ótimo! Com , nossa expressão zerou, o que significa que a igualdade será válida e é uma raiz da nossa equação.
Agora sim, vamos a Briot Ruffini, com esse método vamos reescrever nossa equação como uma multiplicação de , onde esse é a raiz que conhecemos, vezes um outro polinômio de grau menor. No nosso caso, teremos:
Vou ensinar um passo-a-passo pra usar esse método então:
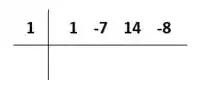
Passo 1: Armar o quadro:
Primeiro, vamos traçar um quadro da seguinte maneira:
Na parte superior esquerda, colocamos a raiz que já conhecemos, no caso, :
Na parte superior direita, colocamos os coeficientes da expressão que queremos reduzir:
Passo 2: Multiplicar e somar
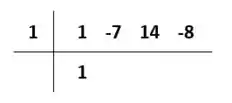
Pra começar, repita o primeiro coeficiente da parte superior direita na parte de baixo:
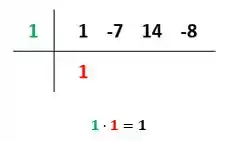
E multiplique o número que desceu pela raiz conhecida:
Agora, some o resultado com o segundo coeficiente à direita e coloque o resultado logo abaixo deste:
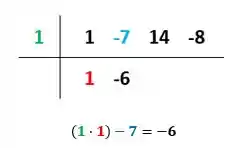
Atenção que como o coeficiente aqui era negativo , a etapa de soma vira uma subtração!
Passo 3: Repetir
Repita o processo até chegar no último coeficiente:
Mais uma vez, pra encerrar:
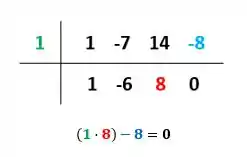
O último termo do resultado é o resto, mas como o resto é zero, não precisamos nos preocupar com ele. Fica tranquilo que a ideia aqui é sempre encontrarmos zero mesmo, então vamos seguir!
Agora, vamos escrever os três números restantes que encontramos como coeficientes de uma expressão do 2º grau:
Essa expressão é o polinômio que estávamos procurando e podemos reescrever nossa equação como:
Portanto, nossas soluções serão:
O resultado da primeira parte, já conhecemos:
Para a segunda, como temos uma equação do 2º grau, vamos usar a fórmula de Bhaskara:
Então, as soluções para nossa equação são
Sei que Briot-Ruffini assusta um pouco da primeira vez que a gente vê, mas treina bastante que vai dar tudo certo!
Briot-Ruffini
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Qual das opções abaixo se refere a uma equação do terceiro grau?
Passo 1
Bom, vamos lá!! Vamos analisar cada uma das opções e verificar qual delas teremos uma equação do terceiro grau?!
Lembrando que em uma equação do terceiro grau precisamos que a maior variável seja a variável elevada ao expoente 3, beleza?!
Passo 2
a) De cara já podemos descartar a letra (a), pois o termo de maior grau é o . Logo, é uma equação do primeiro grau!
b) Aqui também temos a equação geral de uma equação geral do segundo grau, então não é a opção que estamos procurando!
Passo 3
c) Nessa opção temos . Como podemos verificar qual o grau dessa equação?
Podemos fazer a multiplicação distributiva aqui:
Assim, ficamos com
Ou seja, temos uma equação do segundo grau! Logo, não é a opção que estamos procurando!
Passo 4
d) Bom... só nos resta essa opção. Vamos verificar se de fato essa é uma equação do terceiro grau? Como temos podemos fazer a distributiva.
- Primeiro faremos a multiplicação da parte que está em vermelho
- Agora faremos a multiplicação da parte azul e em seguida da amarela
Fazendo a multiplicação dos termos em vermelho, temos
Ficando com
OPA!! Já vimos que surgiu um termo ali que é o de maior grau da equação! Então, encontramos a nossa equação do terceiro grau!
Se quiser podemos dar uma arrumada e somar os termos que tem na equação que encontamos
Ou seja, a nossa resposta é a letra (d)!!
Resposta
Exercício Resolvido #2
Elaboração Própria
Verifique se o conjunto é solução da equação
Passo 1
Bom, vamos lá! Queremos verficar se os números , , e são raízes da equação
Certo?
Opaaaa, mas o que significa mesmo um número ser raíz de uma equação??
Basicamente raíz é o valor que suas variáveis assumem de forma que a igualdade seja verdade. Beleza?!
No caso aqui temos que achar mostrar que ao substituir os valores dados na equação, o resultado dará !
Passo 2
Então vamos substituir os valores que foram dados e verificar se serão raízes!
Para : Ao substituir o valor de na equação
Temos
Se você reparar, é a mesma coisa que multiplicarmos o quatro vezes, assim:
Assim, voltando a nossa equação
Ou seja, o é raíz da equação!
Passo 3
Para iremos realizar o mesmo procedimento! Ao substituir o valor de na equação
Temos
Se você reparar, é a mesma coisa que multiplicarmos o quatro vezes, assim:
Assim, voltando a nossa equação
Ou seja, o também é raíz da equação!
Passo 4
Vamos continuar! Agora para o valor de . Ao substituir o valor de na equação
Temos
Se você reparar, é a mesma coisa que multiplicarmos o quatro vezes, assim:
Assim, voltando a nossa equação
Ou seja, o também é raíz da equação!
Passo 5
Vamos continuar! Agora para o valor de . Ao substituir o valor de na equação
Temos
Se você reparar, é a mesma coisa que multiplicarmos o quatro vezes, assim:
Assim, voltando a nossa equação
Ou seja, o é raíz da equação!
Como todos os valores são raízes, o conjunto é solução da equação!
Resposta
O conjunto é solução da equação!
Exercício Resolvido #3
Elaboração Própria
Temos como raíz da equação o número . Assim, determine o valor do coeficiente .
Passo 1
Vamos lá! Queremos encontrar o valor de . Sabemos que é raíz da equação, então vamos utilizar essa informação a nosso favor para encontrar o valor de !
Como é raíz da equação, vamos substituir esse valor no lugar de ! Assim,
Fazendo a continha e somando o que der pra somar,
Passo 2
Agora vamos encontrar isolar !! Somando ambos os lados da equação por temos
Fazendo as continhas,
Beleza?! Podemos dividir ambos os lados da equação por . Assim,
que é a mesma coisa que
Ouuuu seja, encontramos o nosso valor de que satisfaz as condições do enunciado!!
Resposta
Exercício Resolvido #4
Elaboração Própria
Encontre as raízes da equação abaixo
Passo 1
Bom, vamos lá! Queremos encontrar as raízes da equação de terceiro grau
Certo? Como podemos atacar esse exercício?? Se você reparar, todos os termos da equação possuem . Assim, vamos colocar a expressão entre parênteses, com o comum de todos os termos do lado de fora
Agora, podemos observar duas coisas importantes! A primeira é que, como temos um sozinho do lado de fora, se , toda a expressão será zerada independente do valor que tivermos dentro do parêntese. Isso significa que é uma das soluções da nossa equação!
Beleeeza, já encontramos uma das raízes. Vamos encontrar as outras?
Passo 2
O que sobrou dentro dos parênteses é uma equação do 2 grau, que podemos resolver com a fórmula de Bhaskara para encontrar as outras raízes!
Utilizaremos a fórmula de Bhaskara
Beleza?!
Primeira coisa que precisamos fazer é identificar quem é o , e . Lembra da carinha da nossa equação do 2º grau? Ela tem essa carinha aqui
Então, comparando com a nossa equação
Conseguimos encontrar os valores de , e :
Beleza?! Agora vamos utilizar esses valores para encontrar o :
Substituindo os valores , e , temos
Fazendo as continhas, temos
Passo 3
Agora podemos substituir o valor de e os demais valores na fórmula de Bhaskara:
Teremos então duas raízes:
E
Beleeeza?!
Portanto, as raízes da equação são e !
Resposta
e
Exercício Resolvido #5
Elaboração Própria
Encontre as raízes da equação abaixo
Passo 1
Fala aííí!! Vamos encontrar as raízes dessa equação do terceiro grau?? Se você reparar, não temos o em todos os termos da equação, então não podemos usar aquele método de colocar em evidência o em comum a todos os termos...
Então como podemos atacar esse exercício?? Utilizaremos o processo de Briot-Ruffini! Com ele conseguiremos reduzir o grau do nosso polinômio até chegar numa equação que conseguimos resolver!!
Para usá-lo, precisamos conhecer pelo menos uma raiz da expressão que queremos reduzir o grau. Nesse caso, vamos testar alguns valores de e ver se damos sorte:
Vamos primeiro testar
Substituindo o valor, temos
Opa, essa igualdade não é verdade! . Logo, não é raíz dessa equação!
Vamos testar
Substituindo o valor, temos
Opaaaaa, com , nossa expressão zerou, o que significa que a igualdade será válida e é uma raiz da nossa equação.
Passo 2
Agora sim, vamos a Briot Ruffini, com esse método vamos reescrever nossa equação como uma multiplicação de , onde esse é a raiz que conhecemos, vezes um outro polinômio de grau menor. No nosso caso, teremos:
Beleza?! Então vamos lá! Primeira coisa que faremos é armar o quadro:
Na parte superior esquerda, colocamos a raiz que já conhecemos, no caso, :
Na parte superior direita, colocamos os coeficientes da expressão que queremos reduzir:
Agora, vamos repetir o primeiro coeficiente da parte superior direita na parte de baixo:
E multiplicar o número que desceu pela raiz conhecida:
Agora, some o resultado com o segundo coeficiente à direita
e coloque o resultado logo abaixo deste:
Beleza?!
Agora vamos repetir o processo até chegar no último coeficiente:
Agora o resultado da multiplicação somamos com o terceiro coeficiente à direita
E colocaremos o resultado logo abaixo deste:
Mais uma vez, pra encerrar:
Fazendo a multiplicação, temos
O resultado multiplicaremos com somamos com o quarto coeficiente à direita
E colocaremos o resultado logo abaixo deste:
O último termo do resultado é o resto, mas como o resto é zero, não precisamos nos preocupar com ele. Fica tranquilo que a ideia aqui é sempre encontrarmos zero mesmo, então vamos seguir!
Agora, vamos escrever os três números restantes que encontramos como coeficientes de uma expressão do 2º grau:
Essa expressão é o polinômio que estávamos procurando e podemos reescrever nossa equação como:
Portanto, nossas soluções serão:
O resultado da primeira parte, já conhecemos:
Para a segunda, como temos uma equação do 2º grau, vamos usar a fórmula de Bhaskara:
Beleza?!
Primeira coisa que precisamos fazer é identificar quem é o , e . Lembra da carinha da nossa equação do 2º grau? Ela tem essa carinha aqui
Então, comparando com a nossa equação
Conseguimos encontrar os valores de , e :
Beleza?! Agora vamos utilizar esses valores para encontrar o :
Substituindo os valores , e , temos
Fazendo as continhas, temos
Passo 3
Agora podemos substituir o valor de e os demais valores na fórmula de Bhaskara:
Teremos então duas raízes:
E
Então, as soluções para nossa equação são
Resposta
Exercício Resolvido #6
Elaboração Própria
A soma das soluções da equação é:
- 3
- -2
- -3
- 4
- 0
Passo 1
Bom, vamos lá! Queremos encontrar as raízes da equação de terceiro grau , certo? Se você reparar, todos os termos da equação possuem . Assim, vamos colocar a expressão entre parênteses, com o comum de todos os termos do lado de fora
Agora, podemos observar duas coisas importantes! A primeira é que, como temos um sozinho do lado de fora, se , toda a expressão será zerada independente do valor que tivermos dentro do parêntese. Isso significa que é uma das soluções da nossa equação!
Beleeeza, já encontramos uma das raízes. Vamos encontrar as outras?
Passo 2
O que sobrou dentro dos parênteses é uma equação do 2 grau, que podemos resolver com a fórmula de Bhaskara para encontrar as outras raízes!
Utilizaremos a fórmula de Bhaskara
Beleza?!
Primeira coisa que precisamos fazer é identificar quem é o , e . Lembra da carinha da nossa equação do 2º grau? Ela tem essa carinha aqui
Então, comparando com a nossa equação
Conseguimos encontrar os valores de , e :
Beleza?! Agora vamos utilizar esses valores para encontrar o :
Substituindo os valores , e , temos
Fazendo as continhas, temos
Passo 3
Agora podemos substituir o valor de e os demais valores na fórmula de Bhaskara:
Teremos então duas raízes:
E
Beleeeza?!
Portanto, as raízes da equação são e !
Passo 4
Como a questão pede a soma das soluções, basta somarmos as raízes que encotramos:
Portanto, nossa resposta é a letra (c)
Resposta
Exercício Resolvido #7
Elaboração Própria
Quais das opções abaixo são raízes da equação
- 1,2,-1
- -1,-2,1
- 1,-2,1
- -1,-2,-1
Passo 1
Fala aííí!! Vamos encontrar as raízes dessa equação do terceiro grau?? Se você reparar, não temos o em todos os termos da equação, então não podemos usar aquele método de colocar em evidência o em comum a todos os termos...
Então como podemos atacar esse exercício?? Utilizaremos o processo de Briot-Ruffini! Com ele conseguiremos reduzir o grau do nosso polinômio até chegar numa equação que conseguimos resolver!!
Para usá-lo, precisamos conhecer pelo menos uma raiz da expressão que queremos reduzir o grau. Nesse caso, vamos testar alguns valores de e ver se damos sorte:
Vamos primeiro testar
Substituindo o valor, temos
Opa, essa igualdade não é verdade! . Logo, não é raíz dessa equação!
Vamos testar
Substituindo o valor, temos
Opaaaaa, com , nossa expressão zerou, o que significa que a igualdade será válida e é uma raiz da nossa equação.
Passo 2
Agora sim, vamos a Briot Ruffini, com esse método vamos reescrever nossa equação como uma multiplicação de , onde esse é a raiz que conhecemos, vezes um outro polinômio de grau menor. No nosso caso, teremos:
Beleza?! Então vamos lá! Primeira coisa que faremos é armar o quadro:
Na parte superior esquerda, colocamos a raiz que já conhecemos, no caso, :
Na parte superior direita, colocamos os coeficientes da expressão que queremos reduzir:
Agora, vamos repetir o primeiro coeficiente da parte superior direita na parte de baixo:
E multiplicar o número que desceu pela raiz conhecida:
Agora, some o resultado com o segundo coeficiente à direita
e coloque o resultado logo abaixo deste:
Beleza?!
Agora vamos repetir o processo até chegar no último coeficiente:
Agora o resultado da multiplicação somamos com o terceiro coeficiente à direita
E colocaremos o resultado logo abaixo deste:
Mais uma vez, pra encerrar:
Fazendo a multiplicação, temos
O resultado multiplicaremos com somamos com o quarto coeficiente à direita
E colocaremos o resultado logo abaixo deste:
O último termo do resultado é o resto, mas como o resto é zero, não precisamos nos preocupar com ele. Fica tranquilo que a ideia aqui é sempre encontrarmos zero mesmo, então vamos seguir!
Agora, vamos escrever os três números restantes que encontramos como coeficientes de uma expressão do 2º grau:
Essa expressão é o polinômio que estávamos procurando e podemos reescrever nossa equação como:
Portanto, nossas soluções serão:
O resultado da primeira parte, já conhecemos:
Para a segunda, como temos uma equação do 2º grau, vamos usar a fórmula de Bhaskara:
Beleza?!
Primeira coisa que precisamos fazer é identificar quem é o , e . Lembra da carinha da nossa equação do 2º grau? Ela tem essa carinha aqui
Então, comparando com a nossa equação
Conseguimos encontrar os valores de , e :
Beleza?! Agora vamos utilizar esses valores para encontrar o :
Substituindo os valores , e , temos
Fazendo as continhas, temos
Passo 3
Agora podemos substituir o valor de e os demais valores na fórmula de Bhaskara:
Teremos então duas raízes:
E
Então, as soluções para nossa equação são
Logo, a resposta é a letra (B)
Resposta
Exercício Resolvido #8
Elaboração Própria
O cubo de um número com o seu quadrado é igual e ele mesmo. Que número é esse?
Passo 1
Vamos lá! Para resolver esse problema primeiro precisamos compreender o enunciado e depois vamos montar a equação para encontrar o número.
O cubo um número que não conhecemos com o seu quadrado é igual ele mesmo. Chamaremos esse número de . Escrevendo a equação, teremos
Concorda?!
Ou seja, as raízes dessa equação será a nossa resposta!!
Passo 2
Podemos passar o para o lado esquerdo para todos os termos ficarem do mesmo lado da equação. Assim
Beleza?!
Se você reparar, todos os termos da equação possuem . Assim, vamos colocar a expressão entre parênteses, com o comum de todos os termos do lado de fora
Agora, podemos observar duas coisas importantes! A primeira é que, como temos um sozinho do lado de fora, se , toda a expressão será zerada independente do valor que tivermos dentro do parêntese. Isso significa que é uma das soluções da nossa equação!
Beleeeza, já encontramos uma das raízes. Vamos encontrar as outras?
O que sobrou dentro dos parênteses é uma equação do 2 grau, que podemos resolver com a fórmula de Bhaskara para encontrar as outras raízes!
Utilizaremos a fórmula de Bhaskara
Beleza?!
Passo 3
Agora vamos encontrar as raízes da equação as raízes da equação
Como temos uma equação do 2º grau, vamos usar a fórmula de Bhaskara:
Beleza?!
Primeira coisa que precisamos fazer é identificar quem é o , e . Lembra da carinha da nossa equação do 2º grau? Ela tem essa carinha aqui
Então, comparando com a nossa equação
Conseguimos encontrar os valores de , e :
Beleza?! Agora vamos utilizar esses valores para encontrar o :
Substituindo os valores , e , temos
Fazendo as continhas, temos
Passo 4
Agora podemos substituir o valor de e os demais valores na fórmula de Bhaskara:
Assim, temos como raízes
Então, os números que satisfazem a condição do nosso exercício são e
Resposta
e
Exercício Resolvido #9
Elaboração Própria
Quais são as raízes da equação de quarto grau abaixo?
Passo 1
Opaaaaa! Queremos encontrar as raízes dessa equação de quarto grau, certo? Para isso, utilizaremos o processo de Briot-Ruffini! Com ele conseguiremos reduzir o grau do nosso polinômio até chegar numa equação que conseguimos resolver!!
Para usá-lo, precisamos conhecer pelo menos uma raiz da expressão que queremos reduzir o grau. Nesse caso, vamos testar alguns valores de e ver se damos sorte:
Vamos primeiro testar
Substituindo o valor, temos
Opa, essa igualdade não é verdade! . Logo, não é raíz dessa equação!
Vamos testar
Substituindo o valor, temos
Opaaaaa, com , nossa expressão zerou, o que significa que a igualdade será válida e é uma raiz da nossa equação.
Passo 2
Agora sim, vamos a Briot Ruffini!! Com esse método vamos reescrever nossa equação como uma multiplicação de , onde esse é a raiz que conhecemos, vezes um outro polinômio de grau menor. No nosso caso, teremos:
Beleza?! Então vamos lá! Primeira coisa que faremos é armar o quadro:
Na parte superior esquerda, colocamos a raiz que já conhecemos, no caso, :
Na parte superior direita, colocamos os coeficientes da expressão que queremos reduzir:
Agora, vamos repetir o primeiro coeficiente da parte superior direita na parte de baixo:
E multiplicar o número que desceu pela raiz conhecida:
Agora, some o resultado com o segundo coeficiente à direita
e coloque o resultado logo abaixo deste:
Beleza?!
Agora vamos repetir o processo até chegar no último coeficiente:
Agora o resultado da multiplicação somamos com o terceiro coeficiente à direita
E colocaremos o resultado logo abaixo deste:
Continuando utilizando o mesmo raciocínio...
Fazendo a multiplicação, temos
O resultado somamos com o quarto coeficiente à direita
E colocaremos o resultado logo abaixo deste:
Pra encerrar...
Fazendo a multiplicação, temos
O resultado somamos com o quinto coeficiente à direita
E colocaremos o resultado logo abaixo deste:
O último termo do resultado é o resto, mas como o resto é zero, não precisamos nos preocupar com ele. Fica tranquilo que a ideia aqui é sempre encontrarmos zero mesmo, então vamos seguir!
Agora, vamos escrever os três números restantes que encontramos como coeficientes de uma expressão do 2º grau:
Que é a mesma coisa que
Beleza... Tínhamos uma equação do 4º grau, achamos uma das raízes que é e ao utilizar Briot Ruffini conseguimos reduzir para uma equação do 3º grau. E agora??
Passo 3
Agora nós utilizaremos novamente Briot Ruffini na equação do terceiro grau
Assim, precisamos conhecer pelo menos uma raiz da expressão que queremos reduzir o grau. Nesse caso, vamos testar novamente alguns valores de e ver se damos sorte.
Vamos testar novamente o :
Substituindo os valores
OPAAAAA! De cara já encontramos uma raíz da equação de terceiro grau. O também é raíz dessa equação!
Agora podemos montar o quadrinho e utilizar novamente Briot Ruffini:
Ao repetir o processo, achamos a equação
Show de bola?!
Passo 4
Tá acabando!! Agora só falta encontrarmos as raízes da equação
Como temos uma equação do 2º grau, vamos usar a fórmula de Bhaskara:
Beleza?!
Primeira coisa que precisamos fazer é identificar quem é o , e . Lembra da carinha da nossa equação do 2º grau? Ela tem essa carinha aqui
Então, comparando com a nossa equação
Conseguimos encontrar os valores de , e :
Beleza?! Agora vamos utilizar esses valores para encontrar o :
Substituindo os valores , e , temos
Fazendo as continhas, temos
Passo 5
Agora podemos substituir o valor de e os demais valores na fórmula de Bhaskara:
Encontramos a raíz então para a equação do segundo grau.
Então, as soluções para nossa equação são .