Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Método de Eliminação – Caso Não Homogêneo

Ver Todos os Exercícios

Teoria

Nos tópicos anteriores nós vimos os métodos para resolver sistemas de EDOs homogêneos. Mas e se o sistema não for homogêneo? Olha esse exemplo:

  x ' = x + 4 y + t y ' = x + y + 2 t

Aqui, temos uma função de t , a forma geral do sistema é

X ' = A X + g t

Mas agora a função g ( t ) vai ser

g t = t 2 t

E não nula como quando era um sistema homogêneo. Beleza, mas como vamos resolver isso?

É igual fizemos para o caso homogêneo.

Nosso objetivo é transformar o sistema em apenas uma EDO de 2 ordem, ou em x ou em y, como for mais simples. Se escolhermos o y , como vai ficar?

Vamos isolar z em uma das duas equações, por exemplo na segunda.

x = y ' - y - 2 t

Agora vamos derivar implicitamente essa equação em relação a t , encontrando:

x ' = y ' ' - y ' - 2

Agora substituímos na segunda a derivada e a equação com y isolado.

x ' = x + 4 y + t

y ' ' - y ' - 2 = y ' - y - 2 t + 4 y + t

y ' ' - 2 y ' - 3 y = - t + 2

Pronto! Chegamos no objetivo de encontrar uma EDO de 2 ordem.

Já sabemos resolver esse tipo de EDO, mas vamos dar uma lembrada do passo a passo para essa EDO.

  1. Resolva a equação homogênea (fazendo o f t = 0 ).
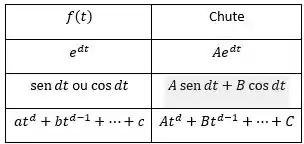
  2. Identifique quem é o f ( t ) e compare com a tabela para determinar o seu chute.

    3. f ( t )

    Chute

    e d t

    A e d t

    sen ⁡ d t ou cos ⁡ d t

    A sen ⁡ d t + B cos ⁡ d t

    a t d + b t d - 1 + … + c

    A t d + B t d - 1 + … + C

  3. Compare a solução homogênea e a particular. Se a solução particular estiver dentro da solução homogênea, multiplicá-la por x . Repetir esse passo até que a solução particular não esteja mais na solução homogênea.
  4. Aplique o chute e suas derivadas na EDO para descobrir as constantes presentes nele, para assim, descobrir y p ( x ) .
  5. Fazer:

y x = y h x + y p x

A solução daquela EDO do nosso exemplo vai ser:

y = C 1 e - t + C 2 e 3 t - 8 9 + t 3

Agora para achar a função x basta fazer

x = y ' - y - 2 t

x = C 1 e - t + C 2 e 3 t - 8 9 + t 3 ' - C 1 e - t + C 2 e 3 t - 8 9 + t 3 - 2 t

x = - C 1 e - t + 3 C 2 e 3 t + 1 3 - C 1 e - t - C 2 e 3 t + 8 9 - t 3 - 2 t

x = - 2 C 1 e - t + 2 C 2 e 3 t + 11 9 - 7 t 3

Deu para relembrar esse método? Qualquer coisa é só voltar nos tópicos de resolução de EDOs de 2ª ordem.

#PartiuPassar

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Determine a solução do sistema abaixo

x ' = 2 x + y + e 2 t y ' = x + 2 y + 3 e 2 t

Passo 1

Esse nosso sistema é não homogêneo, a primeira coisa que temos que fazer é determinar g t

Repara que temos

g t = e 2 t 3 e 2 t

Beleza a próxima coisa que temos que fazer é resolver o sistema homogêneo, que vai ser

x ' = 2 x + y y ' = x + 2 y

Passo 2

Vamos resolver esse sistema pelo método da eliminação.

A primeira coisa a fazer é isolar uma das variáveis. Vamos isolar y na primeira equação

y = x ' - 2 x

Agora vamos derivar implicitamente

y ' = x ' ' - 2 x '

Passo 3

O próximo passo é substituir y ' e y na segunda equação

x ' ' - 2 x ' = x + 2 x ' - 2 x

x ' ' - 2 x ' = x + 2 x ' - 4 x

x ' ' - 4 x ' + 3 x = 0

Passo 4

Resolvendo essa EDO vamos ter a seguinte equação auxiliar

r 2 - 4 r + 3 = 0

r 1 = 1

r 2 = 3

Esse é o caso onde Δ > 0 então a solução vai ser

x h t = C 1 e t + C 2 e 3 t

Passo 5

Agora temos que encontrar y

y = x ' - 2 x

y t = C 1 e t + C 2 e 3 t ' - 2 C 1 e t + C 2 e 3 t

y t = C 1 e t + 3 C 2 e 3 t - 2 C 1 e t - 2 C 2 e 3 t

y h t = - C 1 e t + C 2 e 3 t

Passo 6

Agora temos que achar a solução particular, lembra que g t vai ser

g t = e 2 t 3 e 2 t

Vamos arrumar g t

g t = 1 3 e 2 t

Aqui temos só uma exponencial, então a solução particular vai ficar

X p = x p y p = a e 2 t

Vamos chamar esse vetor a da seguinte forma

a = A B

Assim fica mais fácil fazer as contas ali na frente.

X p = x p y p = A B e 2 t

Repara que nenhuma dessas paradas está na solução da parte homogênea.

Agora temos que cálculo a derivada dessa parada

Passo 7

A derivada vai ficar

X p ' = x p ' y p ' = 2 A 2 B e 2 t

Passo 8

Agora vamos substituir X p ' e X p no sistema

Vamos primeiro listar as funções aqui para ajudar

x p = A e 2 t

y p = B e 2 t

x p ' = 2 A e 2 t

y p ' = 2 B e 2 t

Substituindo no sistema vamos ter

2 A e 2 t = 2 A e 2 t + B e 2 t + e 2 t 2 B e 2 t = A e 2 t + 2 B e 2 t + 3 e 2 t

Vamos arrumar essas contas

2 A e 2 t = 2 A e 2 t + B e 2 t + e 2 t 2 B e 2 t = A e 2 t + 2 B e 2 t + 3 e 2 t

2 A e 2 t = 2 A + B + 1 e 2 t 2 B e 2 t = A + 2 B + 3 e 2 t

Assim vamos ter a seguinte relação

2 A = 2 A + B + 1

2 B = A + 2 B + 3

Isso nos diz que

B = - 1

A = - 3

Então a solução particular vai ficar

x p = - 3 e 2 t

y p = - e 2 t

Passo 9

A solução desse sistema vai ficar

y = y h + y p

x = x h + x p

Então

y t = - C 1 e t + C 2 e 3 t - e 2 t

x t = C 1 e t + C 2 e 3 t - 3 e 2 t

Resposta

x t = C 1 e t + C 2 e 3 t - 3 e 2 t

y t = - C 1 e t + C 2 e 3 t - e 2 t

Exercício Resolvido #2

William E. Boyce e Richard C. DiPrima, Equações diferenciais elementares e problemas de contorno, 8ª ed., Rio de Janeiro: LTC, 2010, pp. 220, exercício 9 – Modificado

Encontre a solução do problema de valor inicial dado.

x ' = x - 5 y + cos ⁡ t y ' = x - 3 y ,   x 0 = 1 1

Passo 1

Esse nosso sistema é não homogêneo, a primeira coisa que temos que fazer é determinar g t

Repara que temos

g t = cos ⁡ t 0

Beleza a próxima coisa que temos que fazer é resolver o sistema homogêneo, que vai ser

x ' = x - 5 y y ' = x - 3 y

Passo 2

Vamos usar o método da eliminação aqui.

A primeira coisa a fazer é isolar uma das variáveis. Vamos isolar x na segunda equação

x = y ' + 3 y

Agora vamos derivar implicitamente

x ' = y ' ' + 3 y '

Passo 3

O próximo passo é substituir x ' e x na primeira equação

y ' ' + 3 y ' = y ' + 3 y - 5 y

y ' ' + 3 y ' - y ' - 3 y + 5 y = 0

y ' ' + 2 y ' + 2 y = 0

Passo 4

Resolvendo essa EDO vamos ter a seguinte equação auxiliar

r 2 + 2 r + 2 = 0

Vamos ter

Δ = 2 2 - 4.2 = 4 - 8 = - 4 < 0

As soluções da equação vão ser

r 1 = - 2 + 4 i 2 = - 2 + 2 i 2 = - 1 + i

r 2 = - 2 - 4 i 2 = - 2 - 2 i 2 = - 1 - i

A solução da homogênea vai ser

y h t = e - t C 1 cos ⁡ t + C 2 sen ⁡ t

Passo 5

Agora temos que encontrar x

x = y ' + 3 y

x t = e - t C 1 cos ⁡ t + C 2 sen ⁡ t ' + 3 e - t C 1 cos ⁡ t + C 2 sen ⁡ t

x t = - e - t C 1 cos ⁡ t + C 2 sen ⁡ t + e - t - C 1 sen ⁡ t + C 2 cos ⁡ t + e - t 3 C 1 cos ⁡ t + 3 C 2 sen ⁡ t

x t = e - t - C 1 + C 2 + 3 C 1 cos ⁡ t + - C 2 - C 1 + 3 C 2 sen ⁡ t

x h t = e - t 2 C 1 + C 2 cos ⁡ t + - C 1 + 2 C 2 sen ⁡ t

Passo 6

Agora temos que achar a solução particular, lembra que g t vai ser

g t = cos ⁡ t 0

A solução particular vai ficar

X p = x p y p = a cos ⁡ t + b sen ⁡ t

Vamos chamar esse vetor a e b da seguinte forma

a = A B

b = C D

Assim fica mais fácil fazer as contas ali na frente.

X p = x p y p = A B cos ⁡ t + C D sen ⁡ t

Repara que nenhuma dessas paradas está na solução da parte homogênea.

Agora temos que cálculo a derivada dessa parada

Passo 7

A derivada vai ficar

X p ' = x p ' y p ' = - A - B sen ⁡ t + C D cos ⁡ t

Passo 8

Agora vamos substituir X p ' e X p no sistema

Vamos primeiro listar as funções aqui para ajudar

x p = A cos ⁡ t + B sen ⁡ t

y p = C cos ⁡ t + D sen ⁡ t

x p ' = - A sen ⁡ t + B cos ⁡ t

y p ' = - C sen ⁡ t + D cos ⁡ t

Substituindo no sistema vamos ter

- A sen ⁡ t + B cos ⁡ t = A cos ⁡ t + B sen ⁡ t - 5 C cos ⁡ t + D sen ⁡ t + cos ⁡ t - C sen ⁡ t + D cos ⁡ t = A cos ⁡ t + B sen ⁡ t - 3 C cos ⁡ t + D sen ⁡ t

Vamos arrumar essas contas

- A sen ⁡ t + B cos ⁡ t = A cos ⁡ t + B sen ⁡ t - 5 C cos ⁡ t - 5 D sen ⁡ t + cos ⁡ t - C sen ⁡ t + D cos ⁡ t = A cos ⁡ t + B sen ⁡ t - 3 C cos ⁡ t - 3 D sen ⁡ t

- A sen ⁡ t + B cos ⁡ t = A - 5 C + 1 cos ⁡ t + B - 5 D sen ⁡ t - C sen ⁡ t + D cos ⁡ t = A - 3 C cos ⁡ t + B - 3 D sen ⁡ t

Assim vamos ter a seguinte relação

- A = B - 5 D

B = A - 5 C + 1

- C = B - 3 D

D = A - 3 C

Somando a primeira equação com a segunda vamos ter

- A = A - 5 C - 5 D + 1

2 A = 5 C + 5 D - 1

Somando a segunda equação com a terceira vamos ter

- C = A - 5 C + 1 - 3 D

A = 4 C + 3 D - 1

Isso nos diz que

2 4 C + 3 D - 1 = 5 C + 5 D - 1

8 C + 6 D - 2 = 5 C + 5 D - 1

3 C = - D + 1

D = - 3 C + 1

Isso nos diz que

A = 4 C + 3 - 3 C + 1 - 1

A = 4 C - 9 C + 3 - 1

A = - 5 C + 2

Substituindo isso na última equação vamos ter

- 3 C + 1 = - 5 C + 2 - 3 C

1 = - 5 C + 2

5 C = 1

C = 1 5

Assim

A = 1

D = - 3 5 + 1 = 2 5

B = 1 - 1 + 1 = 1

Então a solução particular vai ficar

x p = cos ⁡ t + sen ⁡ t

y p = cos ⁡ t 5 + 2 sen ⁡ t 5

Passo 9

A solução desse sistema vai ficar

y = y h + y p

x = x h + x p

Então

x t = e - t 2 C 1 + C 2 cos ⁡ t + - C 1 + 2 C 2 sen ⁡ t + cos ⁡ t + sen ⁡ t

y t = e - t C 1 cos ⁡ t + C 2 sen ⁡ t + cos ⁡ t 5 + 2 sen ⁡ t 5

Passo 10

Agora temos que aplicar o valor inicial que ele nos deu. Sendo assim.

x 0 = 1 × 2 C 1 + C 2 × 1 + - C 1 + 2 C 2 × 0 + 1 + 0 = 1

C 2 = - 2 C 1

y 0 = 1 × C 1 × 1 + C 2 × 0 + 1 5 + 2 × 0 5 = 1

C 1 = 4 5 ,     C 2 = - 8 5

Resposta

x t = - 4 e - t   sen ⁡ t + cos ⁡ t + sen ⁡ t

y t = e - t 4 5 cos ⁡ t - 8 5 sen ⁡ t + cos ⁡ t 5 + 2 sen ⁡ t 5