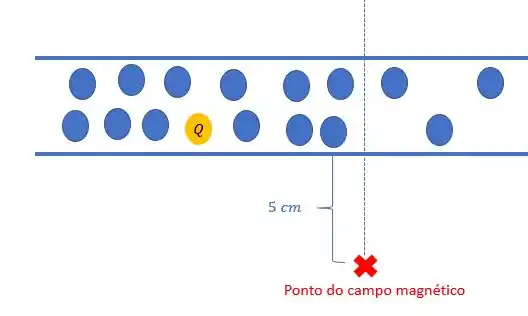
Em um experimento, injetamos uma carga em um fio condutor no meio de diversas outras cargas menores, essa carga em especial viaja a uma velocidade igual a . Desejamos com isso saber o módulo do campo magnético gerado a uma distância igual a do fio quando a carga passar pela linha tracejada, como na figura abaixo:

Despreze a largura do fio.

Vamos começar pelo valor da carga que foi dado no enunciado:

Enquanto a velocidade com a qual essa carga se move é igual a:

E a distância do ponto que desejamos calcular o campo magnético e o fio por onde a carga passa é igual a:

Como está em , a distância deve ser convertida para metros para poder ser usada na fórmula. Fazemos isso andando duas casas para a esquerda que é o mesmo que dividir o valor por :

Um dado que não foi fornecido, mas pode ser deduzido pelo desenho é o ângulo , ele é o ângulo entre a velocidade e a reta da distância, como a velocidade aponta para a direita e a distância aponta para baixo:

Eles formam entre si , logo:

Como vamos precisar do , então:

Substituindo todos os valores na fórmula:

E usando

Nós temos:

Está vendo que temos uma fração que multiplica um número que multiplica outra fração? Podemos resumir isso tudo em uma única fração:

Como temos tanto no numerador quanto no denominador, podemos cortar:

Ficando só com:

Além disso, temos em cima e embaixo. Então também podemos cortar, mas atenção porque na parte de baixo ele está ao quadrado. Então vamos cortar apenas um deles no denominador.

Agora fazemos as contas. Vamos calcular os números e depois as potências de base :

Multiplicando em cima e dividindo por :

Agora vamos olhar multiplicação de potências de bases iguais, onde repetimos a base e somamos os expoentes:

E assim encontramos:

E esse é o módulo do campo magnético gerado pela movimentação dessa carga!