Defeitos Substitucional
Produzido por Erick PinhoTeoria
Faaaaaaala aí!!! Tudo certinho?
Vamos continuar aprendendo sobre defeitos para arrebentarmos nas provas?
Então continue conosco que irá se surpreender como iremos te ajudar!!!!!!
Será que utilizando técnicas altamente sofisticadas conseguimos obter um metal 100% puro?

Impurezas
A resposta para nossa pergunta é: impossível termos um metal 100% puro, ou seja, não é possível, na atualidade, obter um metal que possua somente um tipo de átomo. Logo, impurezas ou átomos diferentes estarão sempre presentes na estrutura cristalina.
Há, também, metais que possuem dois ou mais átomos diferentes compondo a sua estrutura cristalina. Esses metais são conhecidos como ligas, ou seja, adicionam-se elementos diferentes do metal-base para formar um metal com novas características, por exemplo, adiciona-se o estanho no cobre para formar o metal conhecido como bronze. Assim, o cobre terá um aumento significativo em sua resistência mecânica com a adição do estanho.
Adicionar átomos diferentes em uma estrutura cristalina significa dizer que estamos adicionando impurezas a um metal. E não necessariamente o termo “impurezas” significa algo ruim.

Caaaaalma. Vamos entender isso!
Muitas vezes queremos melhorar algumas características do nosso metal base, assim propositalmente adicionamos átomos de impurezas em nossa solução como o exemplo do bronze acima.
Solução?????
Simmmmm, assim como nos líquidos, os sólidos também se tornam uma solução sólida quando adicionamos essas “impurezas”. E aqui, soluto e solvente são termos empregados dá mesma maneira que nos líquidos, ou seja, solvente representa o elemento presente em maior quantidade e soluto representa o elemento em menor concentração. Logo, uma solução sólida apresenta uma única fase!

A figura abaixo é uma representação esquemática bidimensional de átomos de impurezas intersticiais
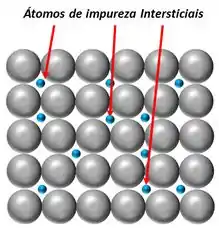
Defeitos pontuais substitucionais
Esse tipo de defeito ocorre quando átomos possuem tamanhos próximos aqueles da matriz com diferenças entre raios menores do que 15% e é caracterizado pela substituição de um átomo da matriz metálica por um átomo de impureza.
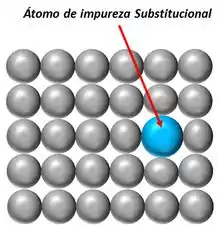
Como podemos observar na figura acima o átomo de impureza Substitucional gera distorção na rede, com isso introduz tensões residuais, atua como barreira ao movimento de discordâncias e aumenta a resistência do material.
Mas fique tranquilo, veremos mais detalhadamente essas mudanças de propriedades em tópicos mais adiantes.
Há algumas características dos átomos do soluto e do solvente que determinam o grau segundo o qual o soluto se dissolve no solvente, também conhecida como regras de Hume-Rothery, para formar uma solução sólida substitucional:
- Fator do tamanho atômico. Como escrito anteriormente, o raio do soluto deve ter tamanho próximo ao do solvente e com uma diferença máxima entre os raios de mais ou menos 15%, caso contrario não irá formar uma solução sólida, mas sim uma segunda fase.
- Estrutura cristalina. Para que tenhamos uma solubilidade sólida apreciável, as estruturas cristalinas de ambos os metais devem ser as mesmas.
- Eletronegatividade. Quanto maior for a diferença de eletronegatividade do soluto e do solvente maior será a probabilidade de formar um composto intermetálico ao invés de uma solução sólida substitucional, ou seja, quanto menor de eletronegatividade maior será a probabilidade de formar solução sólida substitucional.
- Valencias. Sendo iguais todos os demais fatores, um metal apresentará maior tendência de dissolver um outro metal de maior valência do que um metal de menor valência.
Como exemplo, temos uma solução sólida substitucional entre o cobre e o níquel. As ligas de cobre e níquel são conhecidas como cuproniquel, e se caracterizam por apresentarem, em qualquer temperatura solubilidade sólida total, ou seja, em qualquer temperatura o níquel é completamente solúvel no cobre. E essas ligas atender as características para formação de uma solução sólida substitucional.
Vamos checar?
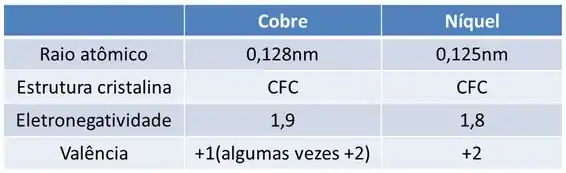
Como podemos notar as ligas cobre e níquel atende todas as características para formar uma solução substitucional!
Para as soluções sólidas intersticiais, como visto, os átomos de impureza preenchem os interstícios que existem no solvente. Para os materiais metálicos que possuem fatores de empacotamento relativamente elevados, ou seja, menores espaços vazios em uma célula unitária, menores deverão ser os átomos de impurezas para que os mesmos ocupem os interstícios.
Uma solução sólida intersticial de exemplo é a solução formada pela adição de carbono ao ferro. O raio atômico do carbono é enquanto o do ferro é .
A figura abaixo é uma representação esquemática bidimensional de um átomo de impureza substitucional, um átomo de impureza intersticial, um átomo de auto intersticial e uma vacância.
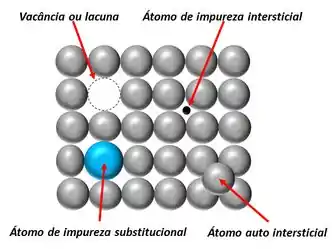
Vamos praticar uma pouco?
Impurezas
Defeitos pontuais substitucionais
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
O que é um defeito substitucional e quais são as características do solvente e do soluto para a formação de uma solução sólida substitucional?
Passo 1
Defeitos substitucional é um tipo de defeito que ocorre quando um átomo de impureza, com tamanho próximo ao do solvente, substitui um átomo da matriz metálica.
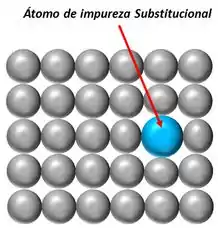
Passo 2
As características do solvente e do soluto para a formação de uma solução sólida substitucional são:
- Tamanho do raio atômico. Para formação de uma solução sólida substitucional é necessário que a diferença entre os raios do soluto e solvente seja em torno de 15%. Caso o átomo de impureza tenha raio maior do que 15% do raio do solvente não haverá formação de uma solução sólida substitucional mas sim um segunda fase.
- Estrutura cristalina. Metais com estutruras cristalinas idênticas possuem uma solubilidade sólida apreciável.
- Eletronegatividade. Quanto menor a diferença de eletronegatividade maior será a probabilidade de formar uma solução sólida substitucional.
- Valencias. Sendo iguais os demais fatores, um metal tendem a dissolver um outro metal de maior valencia do que um metal de menor valencia.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
Aponte os tipos de defeitos pontuais no esquema abaixo.
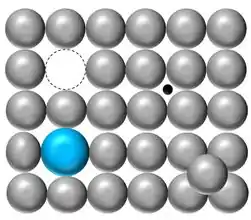
Passo 1
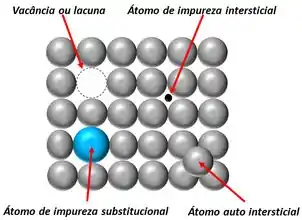
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração própria
Comente sobre a solubilidade do cobre e do níquel para formar uma solução sólida substitucional. Faça o comentário levando em consideração as regras de Hume-Rothery.
Passo 1
As regras de Hume-Rothery são as seguintes:
- Os raios atômicos dos dois elementos não devem diferir em mais de 15%.
- A estrutura cristalina dos elementos devem ser a mesma.
- Eletronegatividade igual ou próxima.
- Valência igual ou próxima.
Passo 2
Agora que descrevemos as regras de Hume-Rothery para a formação de uma solução sólida substitucional, vamos colocar em uma tabela esses dados para compararmos.
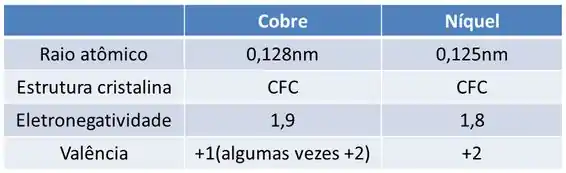
Passo 3
Comparando os dados do Cu com o Ni vemos que: o raio atômico do Ni é 2,3% menor do que o raio atômico do Cu; possuem estruturas cristalinas iguais; eletronegatividade próximas; e valências próximas. Assim, nota-se, baseado nas regras de Hume-Rothery, que as ligas cobre-níquel formam solução sólida substitucional, ou seja, o níquel solubiliza-se totalmente no cobre formando somente uma fase.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Elaboração própria
Tendo o Cu como solvente e o Pb com soluto teremos uma solução solução substiticional? Por que?
Passo 1
Sabemos que as regras de Hume-Rothery nos dizem se dois elementos formarão ou não uma solução sólida substitucional e essas regras são as seguintes:
- Os raios atômicos dos dois elementos não devem diferir em mais de 15%.
- A estrutura cristalina dos elementos devem ser a mesma.
- Eletronegatividade igual ou próxima.
- Valência igual ou próxima.
Passo 2
Vamos anotar os valores do Cu e do Pb
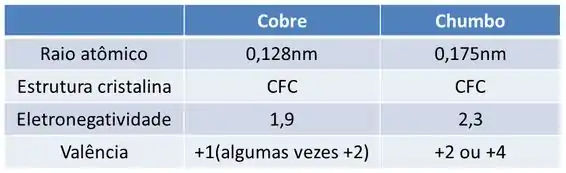
Passo 3
Comparando os dados do Cu com o Pb vemos que: o raio atômico do Pb é 36,7% maior do que o raio atômico do Cu, logo não é necessário continuar verificando as outras regras, uma vez que para raios atômicos maiores do que 15% não haverá formação de solução sólida substitucional, ou seja, o chumbo não é solúvel na matriz de cobre e formará uma segunda fase.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Elaboração própria
O cobre não formará uma solução sólida substitucional completa com a prata. Por que?
Passo 1
As regras de Hume-Rothery nos dizem se dois elementos formarão ou não uma solução sólida substitucional e quão solúveis serão entre si. Essas regras são as seguintes:
- Os raios atômicos dos dois elementos não devem diferir em mais de 15%.
- A estrutura cristalina dos elementos devem ser a mesma.
- Eletronegatividade igual ou próxima.
- Valência igual ou próxima.
Passo 2
Vamos anotar os valores do Cu e da Ag
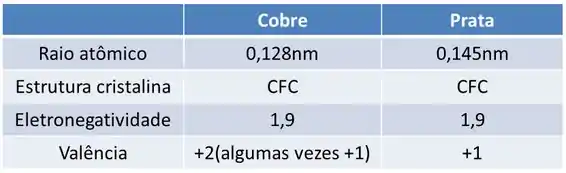
Passo 3
Comparando os dados do Cu com a Ag vemos que: o raio atômico da Ag é 13,3% maior do que o raio atômico do Cu e a valência do cobre é maior do que a da prata. Segundo as regras de Hume-Rothery, quanto maior a diferença dos raios até a faixa de 15% menor será a solubilidade dos elementos. Além disso um metal apresentará maior tendência de dissolver um outro metal de maior valência do que um metal de menor valência, ou seja, o cobre terá menor tendência de dissolver a prata. Devido a esses dois fatores o cobre não formará uma solução sólida substitucional completa com a prata, isto é, o cobre formará uma solução sólida substitucional incompleta com a prata.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.
A seguir, estão tabulados o raio atômico, a estrutura cristalina, a eletronegatividade e as valências mais comuns para vários elementos; para aqueles que não são metais, apenas os raios atômicos estão indicados.
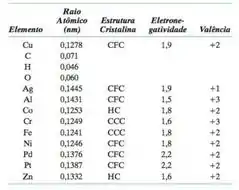
Com quais desses elementos seria esperada a formação do seguinte tipo de composto com o cobre:
- Uma solução sólida substitucional com solubilidade completa?
- Uma solução sólida substitucional com solubilidade incompleta?
- Uma solução sólida intersticial?
Passo 1
- Uma solução sólida substitucional com solubilidade completa ocorre quando: (1) a diferença nos raios atômicos entre o Cu e o outro elemento deve ser menor que ±15%; (2) estrutura cristalina do soluto e do solvente igual; (3) as eletronegatividades devem ser semelhantes em os átomos de soluto e solvente; (4) e as valências devem ser as mesmas, ou próximas.
- Para formar uma solução sólida substitucional de solubilidade incompleta os elementos devem possuir: estrutura cristalina diferente e/ou raio atômico maior do que o cobre e/ou valências diferentes. Portanto os elementos que formam uma solução sólida substitucional com solubilidade incompleta com o cobre são: Ag, Al, Co, Cr, Fe e Zn.
- C, H e O formam solução sólida intersticial, pois apresentam raios atômicos significativamente menores do que o raio atômico do Cu. Logo esses elementos ocuparão os interstícios na rede cristalina do Cu.
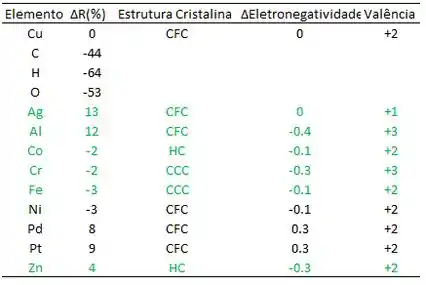
Abaixo segue a tabela destacando esses critérios para os vários elementos:
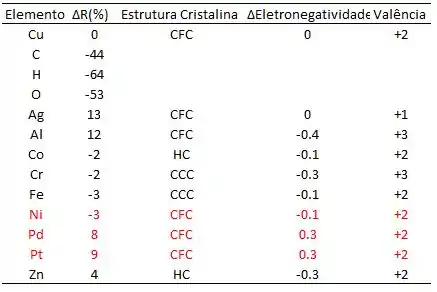
Nota-se na tabela acima que os elementos Ni, Pd e Pt formam uma solução sólida substitucional com solubilidade completa pois apresentam raio atômico com diferença menor do que ±15% em relação ao cobre, mesma estrutura cristalina, diferença de eletronegatividade igual ou próxima ao do cobre e valência igual.
O Co e o Fe possuem transformações alotrópicas da estrutura cristalina para CFC, em temperaturas elevadas, portanto nestas temperaturas o Co e o Fe formam uma solução sólida substitucional com o cobre.
Passo 2
Abaixo segue a tabela destacando-se esses elementos.
Passo 3
Abaixo segue a tabela destacando-se esses elementos.
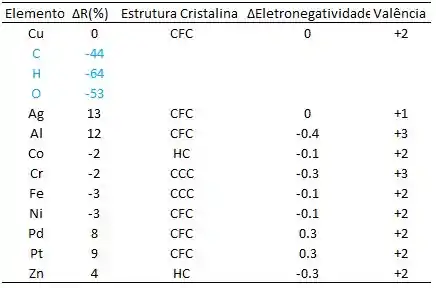
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Elaboração própria
Calcule o raio do maior átomo que pode se situar no interstício octaédrico do Fe CFC, sem deformar a estrutura. Considere o raio do Fe como sendo 0.129nm.
Passo 1
Vamos desenhar uma face da estrutura CFC.
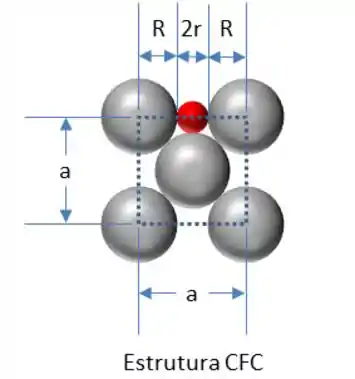
Conforme figura acima vemos que:
–> Equação 1
Nota-se também que:
Passo 2
Agora vamos substituir da equação acima pelo da equação 1 teremos:
Passo 3
Neste passo somente substituímos o valor do raio atômico do Fe para determinarmos o raio do maior átomo que poderá preencher o interstício da estrutura CFC do Fe:
Resposta
Exercício Resolvido #8
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.
Para as estruturas cristalinas CFC E CCC existem dois tipos de sítios intersticiais diferentes. Em cada caso, um sítio é maior que o outro e está normalmente ocupado por átomos de impurezas. Na estrutura CFC, esse sítio maior está localizado no centro de cada umas das arestas da célula unitária; ele é denominado sitio intersticial octaédrico. Por outro lado, na estrutura CCC, o maior tipo de sítio é encontrado nas posições 0 ½ ¼ - isto é, sobre as faces {1 0 0} – e situado sobre essa face a meio caminho entre duas arestas da célula unitária e a um quarto da distância entre as outras duas arestas da célula unitária; ele é denominado sítio intersticial tetraédrico. Tanto para a estrutura cristalina CFC quanto para a estrutura CCC, calcule o raio r de um átomo de impureza que irá se ajustar exatamente nesses sítios, em função do raio atômico R do átomo hospedeiro.
Passo 1
Vamos desenhar uma face da estrutura CFC.
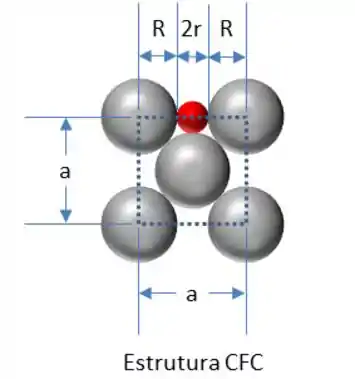
Conforme figura acima vemos que:
–> Equação 1
Nota-se também que:
Substituindo da equação acima pelo da equação 1 teremos:
Passo 2
Agora vamos desenhar uma face da estrutura CCC.
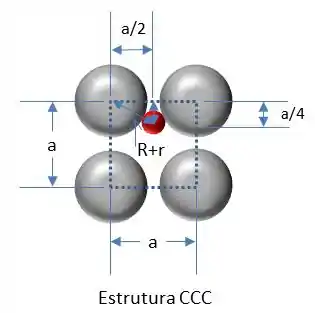
Sabemos, de capítulos anteriores, que o comprimento da célula unitária para a estrutura CCC é:
-> Equação 2
Pela figura acima temos:
Substituindo o valor de da equação 2 na equação acima teremos:
Resolvendo a equação para r:
Como deve ser maior do que zero, então:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #9
Livro Callister, Problema 4.25
Tanto a prata quanto o paládio possuem estrutura cristalina CFC, e o Pd forma uma solução sólida substitucional em concentrações à temperatura ambiente. Calcule o comprimento da aresta da célula unitária para uma liga de 75%p Ag – 25%p Pd. À temperatura ambiente, a massa específica do Pd é de 12,02 g/, e seu peso atômico e raio atômico são 106,4 g/mol e 0,138nm, respectivamente.
Passo 1
Em primeiro lugar, os raios atômicos para Ag e Pd são 0,144 e 0,138 nm, respectivamente. Além disso, usando a relaação , é possível calcular o volume da célula unitária e, como a célula unitária é cúbica, o comprimento da borda da célula unitária é apenas a raiz cúbica do volume. No entanto, é necessário primeiro calcular a densidade e o peso atômico médio dessa liga usando as Equações 4.10a e 4.11a. Na medida em que as densidades de prata e paládio são 10,49 g/(tiradas de dentro da capa) e 12,02 g/, respectivamente, a densidade média é apenas:
E para o peso atômico médio
Passo 2
Agora, o é determinado pela Equação 3.5 como
E, finalmente,
Resposta
Exercício Resolvido #10
Livro Callister, Problema 4.21
O germânio forma uma solução sólida substitucional com silício. Calcule o número de átomos de germânio por centímetro cúbico para uma liga de germânio-silício que contém 15%p Ge e 85%p Si. As massas específicas do germânio puro e do silício puro são de 5,32 e 2,33 g/, respectivamente.
Passo 1
Para resolver esse problema, é necessário o emprego da relação , usando os seguintes valores:
Então,
Resposta
Exercício Resolvido #11
Capítulo 4 , Problemas de Projetos, exercício 38 , item P 2
O ferro e o vanádio possuem ambos estrutura cristalina CCC e, à temperatura ambiente, o V forma solução sólida substitucional no Fe para concentrações de até aproximadamente 20%p V. Determine a concentração em porcentagem em peso de V que deve ser adicionada ao ferro para produzir uma célula unitária com comprimento de aresta .
Passo 1
Olá! Tudo bem? Para responder este exercício, primeiro, utilizaremos a relação , isolando , para encontrar o volume da célula unitária, . Então temos:
Onde e são o peso e a densidade atômicos, respectivamente, da liga Fe-V. Na medida em que ambos os materiais têm a estrutura cristalina CCC, que possui simetria cúbica, é apenas o cubo do comprimento da célula unitária, . Isto é:
Passo 2
Agora é necessário construir expressões que relacionem e em termos da concentração de vanádio, , usando as Equações e .
Para , onde e , temos:
Para , onde e , temos:
Passo 3
Agora retornaremos à equação , onde dentro da célula unitária CCC existem átomos equivalentes e, portanto, o valor de na Equação é ; portanto, esta expressão pode ser escrita em termos da concentração de V em da seguinte maneira, levando em consideração todas as fórmulas desenvolvidas:
Resolvemos esta expressão isolando , então temos: