Concentrador de tensão
Produzido por Erick PinhoTeoria
Tudo bem com vocês galerinha?
Introdução aos princípios de mecânica da fratura
A mecânica da fratura é uma disciplina que estuda o comportamento dos materiais partindo do pressuposto que o material possui descontinuidades internas e superficiais inerentes do processo de fabricação.
Em propriedades dos materiais vimos os conceitos de tensão de escoamento, tensão de ruptura, entre outras. Vimos que a tensão de escoamento é a tensão que o material sofre antes da deformação plástica e que a tensão de ruptura é a tensão na qual o material sofre a ruptura. As equações que representa essas tensões são:
Onde é a tensão de escoamento, é a Força normal, é a força normal de ruptura e é área do corpo de prova.
Note que ambas as equações são praticamente idênticas mudando somente à força. Mas nestas equações não levamos em consideração descontinuidades internas e superficiais que obviamente estão presentes em todos os materiais, por mais perfeitos que sejam.
Assim, na mecânica da fratura ao calcularmos, por exemplo, a tensão de ruptura do material, iremos levar em consideração imperfeições que podem diminuir a tensão de ruptura nominal, que foi calculada supondo que o material seja perfeito. Por exemplo, suponha que a tensão de ruptura de um material perfeito seja:
Porém, caso o material possua imperfeições, tais como trincas internas, essa tensão de escoamento irá diminuir, por exemplo, .
Note que a nova tensão de escoamento foi o resultado da multiplicação da tensão de escoamento nominal por um fator . Esse fator é conhecido como fator de concentração de tensão.

Caaaaaalma!! Vamos entender melhor o quê é esse tal de concentrador de tensão.
Concentrador de tensão
Já tentaram rasgar uma folha de papel sem nenhum entalhe no meio, como a figura abaixo? Tente!
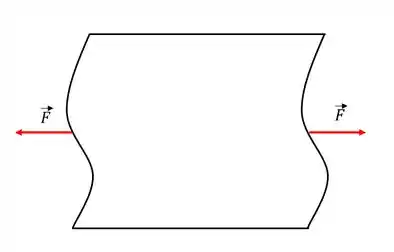
Agora vamos tentar rasgar essa mesma folha de papel, porém agora, faremos um pequeno entalhe no meio, como a figura abaixo.
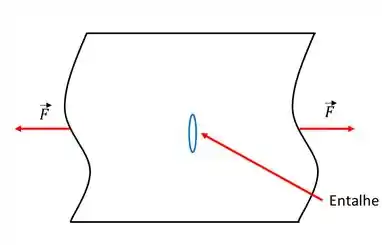
Note que dessa vez iremos conseguir rasgar o papel com uma menor força. Logo, o entalhe que fizemos atuou como um concentrador de tensão, ou seja, a tensão aplicada foi amplificada ou concentrada na extremidade do defeito. A magnitude dessa amplificação depende da orientação e da geometria da trinca. Por exemplo, faça o entalhe, agora, no papel com o raio maior da elipse no mesmo sentido da força, como a figura abaixo.
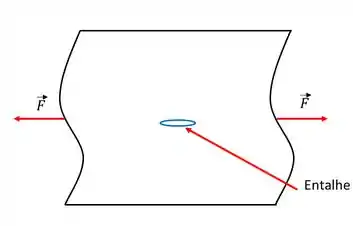
Note que com essa orientação é muito mais difícil romper o papel do que a orientação anterior!!!
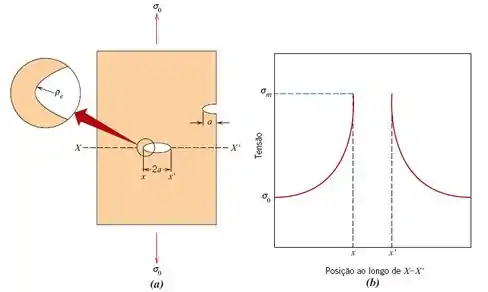
Na figura acima temos uma superfície (a) com dois entalhes: uma no meio e um na borda. Note que a tensão é amplificada para no limite do entalhe, como pode ser observado no gráfico de tensão (b) ao longo de . Observe que a tensão diminui à medida que distancia do entalhe. Em posições mais distantes, a tensão é simplesmente a tensão nominal .
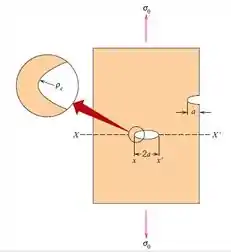
Considerando que uma trinca é semelhante a um orifício elíptico que atravessa uma placa e está orientada perpendicularmente à direção da tensão aplicada, a tensão máxima,ocorre na extremidade da trinca e pode ser aproximada pela expressão:
Em que é a magnitude da tensão de tração nominal aplicada, é o raio de curvatura da extremidade da trinca e é o comprimento de uma trinca superficial, ou metade do comprimento de uma trinca interna.
Esses concentradores de tensões podem ser: vazios, inclusões, arestas vivas, arranhões e entalhes.
Em materiais dúcteis o efeito do concentrador de tensão é suavizado, pois haverá uma distribuição de tensões mais uniforme na vizinhança do concentrador devido à deformação plástica. Sendo assim, a tensão máxima será menor do que a tensão máxima teórica. Já para materiais frágeis o efeito do concentrador de tensão é mais significativo, pois não haverá escoamento e redistribuição das tensões, portanto resultará, essencialmente, a tensão máxima teórica.
Vamos praticar uma pouco?
Concentrador de tensão
Exercícios Resolvidos
Exercício Resolvido #1
Estácio (adaptado)
A abordagem aceitável no dimensionamento de um projeto consiste em determinar o fator de concentração detensões associado a alguma descontinuidade geométrica. Este valor, multiplicado pela tensão nominal, indicao nível de tensões efetivo na região de descontinuidade. O fator de concentração de tensões é uma recurso quantitativo associado à segurança, que poderá ser utilizado pelo projetista.
Com relação a este fator, PODEMOS afirmar:
- .
- .
- .
- .
- .
Passo 1
O concentrador de tensão atua aumentando a tensão nos pontos, nos quais estão localizados. Assim, o concentrador de tensão multiplica a tensão nominal por um fator maior do que 1.
Em que representa a tensão máxima no ponto de concentrador de tensão e representa a tensão nominal. Logo para que a tensão máxima seja maior do que a tensão nomimal deverá ser maior do que 1.
Resposta
Letra: b)
Exercício Resolvido #2
Estácio (adaptado)
As descontinuidades ou mudanças bruscas na seção existente em um elemento estrutural provocam uma redistribuição do campo de tensões e deformações nas suas proximidades em que as linhas do campo de tensão são mais densas nas proximidades da descontinuidade. Neste contexto, é definido o fator de concentração de tensões (), que é um número adimensional, ou seja, sem unidade, e que é dado pela razão entre as tensões. Considerandoas opções a seguir, identifique qual representa CORRETAMENTE o .
Passo 1
O concentrador de tensão atua aumentando a tensão nos pontos, nos quais estão localizados. Assim, o concentrador de tensão multiplica a tensão nominal por um fator maior do que 1.
Em que representa a tensão máxima no ponto de concentrador de tensão e representa a tensão nominal. Logo para que a tensão máxima seja maior do que a tensão nomimal deverá ser maior do que 1.
Logo:
Resposta
Letra: c)
Exercício Resolvido #3
Estácio (adaptado)
A Mecânica da Fratura Elasto-plástica considera que o campo de deformação plástico na ponta da trinca não é desprezível (deformação plástica predominante) e promove efetivamente deformação plástica. A expressão anterior, apresentada por Alan A. Griffith é modificada, assumindo a forma: .Considerando a expressão anterior, identifique o item cuja associação está INCORRETA:
- : é a energia associada a deformação plástica
- : é a energia de superfície específica
- : é a metade do comprimento de uma trinca interna
- : é o modulo de elasticidade
- : é a tensão crítica necessária para a nucleação de uma trinca em um material
Passo 1
A mecânica da fratura leva em consideração que em um material já exista defeitos, por exemplo, trincas, inerentes do processo de produção. Assim, é a tensão crítica necessária para a propagação de uma trinca em um material frágil
Resposta
Letra: e)
Exercício Resolvido #4
Estácio (adaptado)
Assinale a alternativa incorreta:
- O efeito do concentrador de tensão é mais signifivativo nos materiais frágeis que nos dúcteis.
- Em um metal dúctil, a deformação plástica inicia quando a tensão máxima excede o limite de escoamento.
- A distribuição de tensões, em materiais dúcteis, é mais uniforme na vizinhança do concentrador de tensões.
- O desenvolvimento de um fator de concentração de tensões máximo é maior que o valor teórico em materiais dúcteis.
- O escoamento e redistribuição de tensões ocorre em uma extensão apreciável ao redor de defeitos e descontinuidades nos matérias frágeis.
Passo 1
O escoamento e redistribuição de tensões não ocorre em nenhuma extensão apreciável ao redor de defeitos e descontinuidades nos matérias frágeis. Sendo assim, o calculo da concentração de tensões teórica, para materiais frágeis é valida.
Resposta
Letra: e)
Exercício Resolvido #5
Elaboração Própria
Por que a resistência à fratura dos materiais normalmente é menor do que a determinada pelos cálculos teóricos?
Passo 1
Fala ai! A diferença entre os valores experimentais e teóricos de resistência à fratura é explicada pela existência de defeitos ou trincas microscópicas.
Sob condições normais essas imperfeições existem na superfície ou no interior dos materiais sem problema nenhum, mas quando é aplicada uma tensão, ela pode ser aumentada ou concentrada na extremidade do defeito fazendo com que o material acabe fraturando.
Resposta
A diferença entre os valores experimentais e teóricos de resistência à fratura é explicada pela existência de defeitos ou trincas microscópicas.
Exercício Resolvido #6
Elaboração Própria
Quais são os fatores que influenciam na tensão máxima que pode existir em uma trinca?
Passo 1
Fala ai! Pra gente responder essa questão vamos olhar primeiro a fórmula da tensão máxima na extremidade da trinca:
Onde é a tensão aplicada, é o raio de curvatura da extremidade da trinca e é o comprimento da trinca.
Esses são os fatores que influenciam a tensão máxima suportada.
Resposta
A tensão aplicada, o raio de curvatura e o comprimento da trinca.
Exercício Resolvido #7
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição
Uma placa relativamente grande de um vidro é submetida à uma tensão de tração de . Se a energia de superfície e o módulo de elasticidade para esse vidro são de e , respectivamente, determine o comprimento máximo de um defeito de superfície que pode existir sem que ocorra fratura.
Passo 1
Sabe-se que o comprimento de um defeito pode ser dado pela equação abaixo:
Onde, será o comprimento máximo que um defeito de superfície possa existir sem que ocorra fratura.
Passo 2
Rearranjando a equação acima a fim de isolar o
Passo 3
Dados do problema:
Passo 4
Agora vamos substituir os valores fornecidos a fim de calcularmos o comprimento máximo da trinca:
Resposta
Exercício Resolvido #8
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição
Qual é a magnitude da tensão máxima existente na extremidade de uma trinca interna que possui um raio de curvatura de e um comprimento de trinca de quando uma tensão de é aplicada?
Passo 1
Sabe-se que a tensão máxima é dada pela equação abaixo:
Onde, será o comprimento de uma trinca superficial, é a magnitude de tensão de tração nominal aplicada e é o raio de curvatura da extremidade da trinca.
Passo 2
Dados do problema:
Passo 3
Agora vamos substituir os valores fornecidos a fim de calcularmos a magnitude da tensão máxima:
Resposta
Exercício Resolvido #9
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição
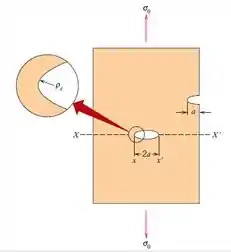
Estime a resistência à fratura teórica de uma material frágil quando se sabe que a fratura ocorre pela propagação de uma trinca superficial de forma elíptica com comprimento de e raio de curvatura de 1 quando é aplicada uma tensão de .
Passo 1
Sabe-se que a tensão máxima é dada pela equação abaixo:
Onde, será o comprimento de uma trinca superficial, é a magnitude de tensão de tração nominal aplicada e é o raio de curvatura da extremidade da trinca.
Passo 2
Dados do problema:
Passo 3
Agora vamos substituir os valores fornecidos a fim de calcularmos a magnitude da tensão máxima:
Resposta
Exercício Resolvido #10
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição
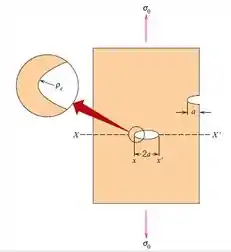
Um componente em poliestireno não deve falhar quando for aplicada uma tensão de tração de . Determine o comprimento máximo admissível para uma trinca superficial se a energia de superfície do poliestireno é de . Assuma um módulo de elasticidade de
Passo 1
Sabe-se que o comprimento de um defeito pode ser dado pela equação abaixo:
Onde, será o comprimento máximo que um defeito de superfície possa existir sem que ocorra fratura.
Passo 2
Rearranjando a equação acima a fim de isolar o
Passo 3
Dados do problema:
Passo 4
Agora vamos substituir os valores fornecidos a fim de calcularmos o comprimento máximo da trinca:
Resposta
Exercício Resolvido #11
Livro Callister, Problema 8.3 Adaptado
Usando os dados abaixo, calcule a tensão crítica necessária para a propagação de uma trinca superficial com comprimento de 0.05mm, se a energia de superfície para um vidro de cal de soda é de .
Módulo de elasticidade do vidro de cal de soda = 69 GPa.
Passo 1
Fala ai! Podemos determinar a tensão crítica necessária para a propagação de uma fissura superficial no vidro de soda-cal considerando o valor de 69 GPa como módulo de elasticidade, obtemos: