Assuma que o ferro comercial () na Tabela 20.5 atinja exatamente o ponto de saturação quando inserido na bobina do Problema 20.1. Calcule a magnetização de saturação.

Fala ai! Pra começar a responder essa questão, vamos dar uma olhada na tabela 20.5 e ver as propriedades do ferro que são dadas pra gente.

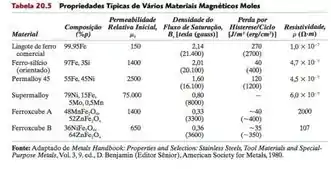
E vamos olhar também o problema 20.1 pra ver que bobina é essa!

Bom, pra resolver essa questão temos que lembrar que:

Onde .

H é definido pela bobina:

Maaaas, tem um pequeno detalhe. A tabela dá pra gente a permeabilidade relativa inicial. Então a gente não pode usar ela, porque queremos saber a magnetização de saturação. O que a gente vai ter que fazer é usar a densidade de fluxo de saturação e a partir dela chegar na nossa permeabilidade relativa, beleza?

Lembrando que a permeabilidade do vácuo é conhecida: .