Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 20.Perguntas e Problemas - Ex. 23
A energia (por unidade de volume) necessária para magnetizar um material ferromagnético até a saturação é definida pela seguinte equação:
Ou seja, é igual ao produto de e a área sob uma curve M em função de H, até o ponto de saturação referente ao eixo das ordenadas (ou M) – por exemplo, na Figura 20.17, a área entre o eixo vertical e a curva de magnetização até. Estime os valores de (em J/m³) para um monocristal de níquel nas direções , e
Passo 1
Fala ai! Pra começar a responder essa questão, a gente tem que dar uma olhada no gráfico da magnetização do níquel em algumas direções cristalográficas:
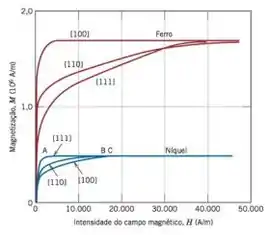
O valor da magnetização de saturação é quando a curva para de subir (ali em ), então a gente pode ver que a área que vamos ter que calcular pra cada direção vai ter um valor diferente. Observando o gráfico temos que os valores de saturação são então aproximadamente:
Passo 2
Pra calcular essa área aproximada, vamos calcular uns retângulos com os valores de M e H. E subtrair a área de alguns triângulos, que vão ser mais ou menos equivalentes ao arredondamento da curva, beleza?
Pro plano , temos que:
Pro plano , temos que:
Pro plano , temos que:
Passo 3
Agora só precisamos multiplicar o valor da área pela permissividade do vácuo, que já é conhecida!
Fazendo as continhas então: