Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 5.Perguntas e Problemas - Ex. 23
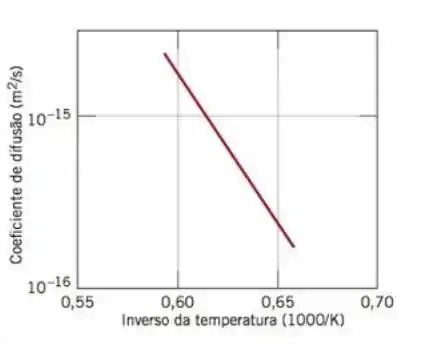
A figura a seguir mostra um gráfico do logaritmo (para a base 10) do coeficiente de difusão em função do inverso da temperatura absoluta, para a difusão do ferro no cromo. Determine os valores para a energia de ativação e para a constante pré exponencial.
Passo 1
Galerinha tudo beleza ? Espero que sim!! Olha só o exercicio pede para que nós possamos encontrar para Qd e Do (difusão), mas se liga em uma coisa, no eixo y temos a variação do coeficiente de difusão ΔD em log que é o fornecido pelo exercício pela variação do tempo (eixo x), então podemos montar a seguinte analogia.
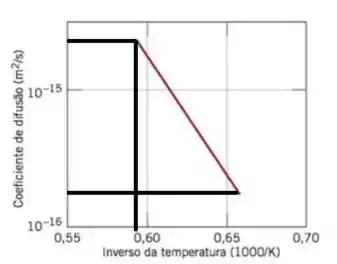
Notem que a temperatura varia conforme a angulatura da reta entre aproximadamente 0,60 e 0,65
Galera mas vale se ligar que o eixo vertical está na escala logarítmica (base 10) então se temos o valor demarcado alí em quase então o logaritmo é D= -14,3 e assim vale para o outro ponto onde o valor é de aproximadamente temos D= -15,8. Agora que determinamos o valores podemos substituir na equação, venha !!
Igualando as equações, podemos agora substituir os valores:
573390 J/mol
Passo 2
Agora podemos calcular DO
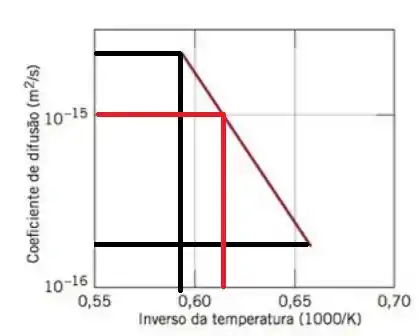
Notem que não temos o valor de D, mas podemos estipular um valor entre os que pontos marcados por nós no gráfico, veja um exemplo
.
Agora podemos substituir considerando o valor de D = 1cuja a temperatura respectiva é de aproximadamente 0,62 , considerando que se trata do inverso da temperatura, temos a temperatura no valor de 1612 K, agora vamos substituir
Resposta
- 573390 J/mol