Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 6.Perguntas e Problemas - Ex. 50
Um corpo de provas de aço, tendo uma seção transversal retangular com dimensões de , possui o comportamento tensão-deformação mostrado na Figura . Se esse corpo de provas for submetido a uma força de tração de então
- Determine os valores para as deformações elástica e plástica.
- Se o seu comprimento original for , qual será seu comprimento final após a carga no item (a) ter sido aplicada e então liberada?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Pessoal, nesse exercício, temos que determinar os valores para as deformações elástica e plástica e depois descobrir o comprimento final da amostra.
Primeiro vamos encontrar a tensão correspondente a uma carga de no nosso corpo de prova:
Onde é a carga e é a área da seção transversal.
Temos que:
Portanto, a tensão pode ser dada por:
Passo 2
Vamos observar no gráfico tensão-deformação do nosso material, onde se encontra a tensão de :
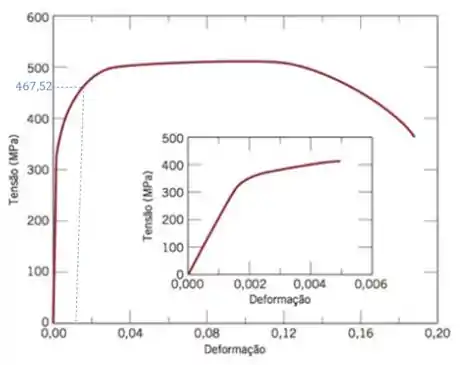
Podemos observar que atingiu a região plástica, portanto teremos deformações elástica e plástica.
A deformação verdadeira é de cerca de :
O valor do módulo de elasticidade pode ser obtido na tabela . Para o aço, temos que:
Passo 3
Portanto, podemos calcular a deformação elástica a partir da lei de Hooke:
O valor da deformação elástica será:
Para o cálculo da deformação plástica, temos que:
O valor da deformação plástica será:
Passo 4
Para o item (b), temos que calcular o comprimento final da amostra após a carga ser liberada.
Temos que:
Como o comprimento inicial é de e a deformação plástica vale , temos que:
Portanto, o comprimento final do corpo após a liberação da carga será: