Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 3.Perguntas e Problemas - Ex. 64
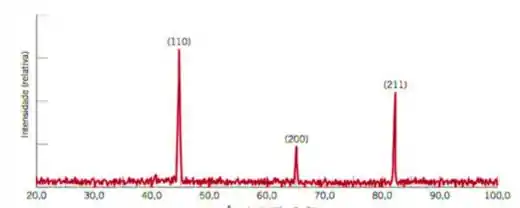
A figura mostra um padrão de difração de raios x para o ferro que foi tomado usando um difratômetro e radiação x monocromática com comprimento de onda de 0,1542 nm. Cada pico de difração no difratograma foi identificado. Calcule o espaçamento interplanar para cada conjunto de planos identificados e determine também o parâmetro de rede do Fe para cada um dos picos.
Passo 1
(110)
Isolando o “d” temos:
nm
0,284
Passo 2
(200)
Isolando o “d” temos:
nm
0,2866
Passo 3
(211)
Isolando o “d” temos:
nm
0,2856
Resposta
nm
0,284
0,2866
0,2856
Exercícios de Livros Relacionados
Os picos de difração estão identificados de acordo com as regras de reflexão para estruturas CCC (isso é a soma h+k+l deve ser par). Cite os índices h,k e l para os quatros primeiros picos de difração
Você esperaria que ao solidificar, um material no qual as ligações atômicas são predominantemente iônicas tenha maior ou menor probabilidade de formar um sólido não cristalino em comparação a um mater
A figura 3.25 mostra os quatros primeiros picos do difratograma de raios x para o cobre, que possui uma estrutura cristalina CFC, foi usada radiação x monocromática com comprimento de onda de 0,1542 n
Se o raio atômico do alumínio é de 0,143 nm, calcule o volume da sua célula unitária em metros cúbicos.