Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 9.Perguntas e Problemas - Ex. 19

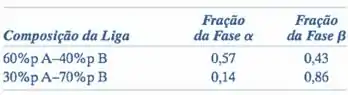
Para ligas de dois metais hipotéticos A e B, existe uma fase α rica em A, e uma fase β, rica em B. A partir das frações mássicas de ambas as fases para duas ligas diferentes dadas na tabela a seguir (e que estão na mesma temperatura), determine a composição da fronteira entre as fase (ou limite de solubilidade) tanto para a fase α quanto para a β nessa temperatura.

Passo 1

  • Primeira Liga

W α 1   =   0,57   = C β   -   C 01 C β   -   C α   = C β   -   60   C β   -   C α = C β   -   C α = C β   -   60   0,57 (1)

W β = 0,43   = C o   -   C α C β   -   C α =   60   -   C α   C β   -   C α   ( 2 )

Substituindo a equação 1 no denominador da equação 2 temos:

0,43   = 60   -   C α   C β   -   60   × 0,57

0,43   × ( C β   -   60 ) = ( 60   -   C α ) × 0,57

0,43   C β   -   25,8 = 34,2   -   0,57 C α

C β   = 139,5   -   1,32 C α (3)

Passo 2

2° Liga

W α 2   =   0,14   = C β   -   C 02 C β   -   C α   = C β   -   30   C β   -   C α = C β   -   C α = C β   -   30   0,14   ( 4 )

W β = 0,86   = C o   -   C α C β   -   C α =   30 -   C α   C β   -   C α   ( 5 )

Substituindo a equação 3 no denominador da equação 4 temos:

0,86   = 30   -   C α   C β   -   30   × 0,14

0,86 × ( C β   -   30 ) = ( 30   -   C α ) × 0,14

0,86   C β   -   25,8 = 4,2   -   0,14 C α (6)

Substituindo a equação 3 na 6 temos:

0,86 ×   ( 139,5   -   1,32 C α )     -   25,8 = 4,2   -   0,14 C α

120   -   1,135 C α     -   25,8 = 4,2   -   0,14 C α

-   1,135 C α +   0,14 C α     = 4,2 - 94,2

-   1,135 C α +   0,14 C α     = - 90

C α = 90,5 %   A   e   10 %     B

Passo 3

Agora que achamos C α vamos substituir o valor na equação 3.

C β   = 139,5   -   1,32 × 90,5 (3)

C β   = 20,1   %   A   e   79,9 % B  

Resposta

C α = 90,5 %   A   e   10 %     B

C β   = 20,1   %   A   e   79,9 % B  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cite as fases presentes e as composições das fases para as seguintes ligas:(a) 90 % p Zn- 10 % p Cu a 400 ° C( 750 ° F ) (b) 75 % p Sn- 25 % p Pb a 175 ° C( 345 ° F ) (c) 55 % p Ag- 45 % p Cu a 900 °
É possível existir uma liga de cobre-zinco que, em equilíbrio, consista em uma fase ε da composição 80%p Zn-20% p Cu, e também em uma fase líquida da composição em 95%p Zn-5% p Cu? Se isso for possíve
É possível haver uma liga de cobre-níquel que, em equilíbrio, consiste em uma fase líquida da composição 20% p Ni-80% p de Cu e também em uma fase α da composição em 37%p de Ni-63%p de Cu? Se isso for
Uma liga de cobre-níquel da composição 70%p Ni-30%p Cu é aquecida lentamente a partir de uma temperatura de 1300 ° C (2370 ° F). Em qual temperatura se forma a primeira fase líquida? Qual é a composiç
Uma liga de 50% p Pb-50% p Mg é resfriada lentamente de 700 ° C (1290 ° F) até 400 ° C (750 ° F).Em qual temperatura se forma a primeira fase sólida? Qual é a composição desta fase sólida? Em qual tem