Uma liga de 90% p Ag-10% p Cu é aquecida até uma temperatura na região das fases β + líquido. Se a composição da fase líquida for 85%p Ag, Determine:
a) A temperatura da liga
b) A composição da fase β
c) As frações de mássicas de ambas as fases
Passo 1
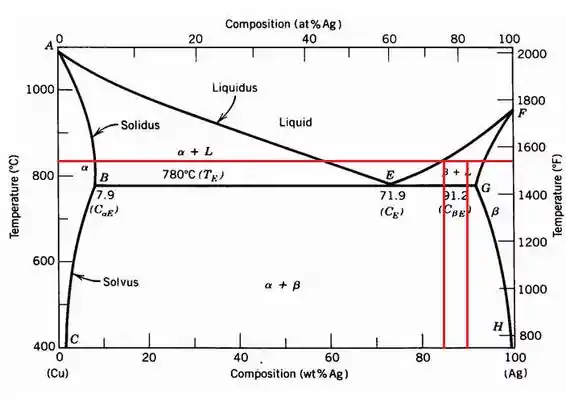
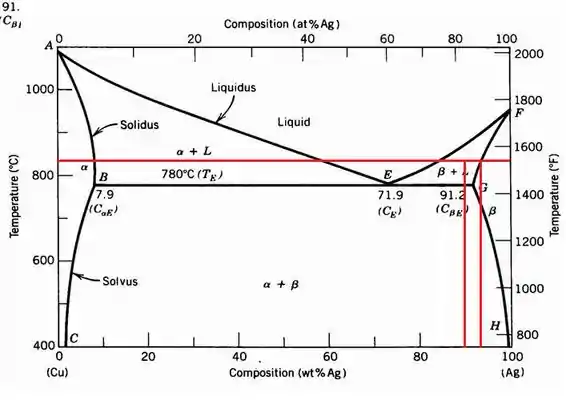
- Para determinarmos a temperatura precisamos construir uma linha de ligação entre a fase β e a fase L, onde L tem composição 85%p Ag e a liga tem 90%.
- A composição da fase β a esta temperatura é determinada a partir da interseção desta mesma linha de ligação com a linha sólidus, que corresponde a cerca de 93% Ag.
- Para calcularmos as frações mássicas das duas vamos usar a regra da alavanca
 INCLUDEPICTURE "https://pt-static.z-dn.net/files/de5/d08e65e22571550fbcc6be627bb67799.png" \* MERGEFORMATINET
INCLUDEPICTURE "https://pt-static.z-dn.net/files/de5/d08e65e22571550fbcc6be627bb67799.png" \* MERGEFORMATINET
A linha intercepta em 85%p Ag a cerca de 830 ° C.
Passo 2
Passo 3
C0 = 90% Ag
CL = 85% Ag
Cβ = 93% Ag
Resposta
- 95% Ag
- ;