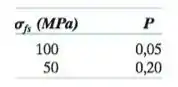
A resistência à flexão e a fração volumétrica da porosidade a ela associada para duas amostras do mesmo material cerâmico são as seguintes:
(a)Calcule a resistência à flexão para uma amostra desse material completamente sem porosidade.
(b)Calcule a resistência para uma fração volumétrica da porosidade de 0,10.
Passo 1
Beleza galerinha, lets go! (do húngaro para vamos lá). Nessa questão temos que calcular a resistência para duas situações. Nesse caso, vamos primeiro resolver o item (a). Temos que determinar a resistência à flexão de um material não poroso. Se o logaritmo natural for tomado de ambos os lados da Equação 12.10, temos o seguinte:
Primeiro temos a eq. 12.10:
Passando o nosso lnzinho que vai facilitar nossa vida:
Passo 2
Usando os dados fornecidos na declaração do problema, duas equações simultâneas podem ser escritas como,
E agora? Sistemas! Resolvendo o sistema para e para , temos que:
Para o material não poroso, (você pode ler mais sobre a constante de porosidade na seção 4 do capítulo 12 desse mesmo livro, okay?). Logo, se o material é não poroso, da equação 12.10, temos . Portanto a resistência à flexão, , para o material não poroso é:
Passo 3
Agora vamos passar para o item (b)! Temos que achar para um novo valor de . E vai ser tranquilo galera! Basta pegarmos os valores que achamos no passo 2, e aplicarmos novamente na fórmula (Eq. 12.10)!
Logo,
Legal né !? Agora que você respondeu a ultima questão do capítulo, repete todas as questões do capítulo aqui no Responde Aí mais uma vez só pra memorizar.

Hahahahaha, tô brincando!