Dispomos da seguinte mistura Benzeno – Tolueno:

Desejamos separar essas duas misturas em uma coluna de destilação que opera a , para obter um produto de topo líquido rico em benzeno () com e um resíduo contendo de benzeno que deixa o último prato da coluna.
Determine o número de estágios teóricos necessários para a separação, nessas condições e com volatilidade relativa igual a e .
Passo 1
Primeiro passo em questões de coluna de destilação é desenhar a coluna e o segundo será fazer o balanço de massa.
Nesse caso, a nossa coluna possui duas cargas e elas irão entrar na coluna por ordem de composição. A mais rica no produto leve de topo ( Carga 1) entra por cima e a mais pobre (Carga 2 ) entra por baixo. Além disso, repara que a a questão informou que o produto de fundo deixa o último prato da coluna ( antes de passar pelo refervedor), então temos um refervedor total 😊 E a nossa representação é essa:
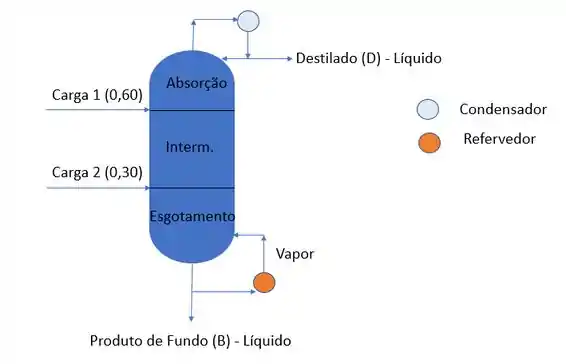
Passo 2
O segundo passo é calcular o balanço de massa para encontrar a composição dos produtos de topo e de fundo. Como tudo que entra é igual a tudo que sai, temos que:
Substituindo, obtemos que:
Portanto, temos duas equações e duas incógnitas e podemos resolver através de sisteminhas. E aí obtemos que:
Guarda com carinho essas vazões que lá na frente vamos utilizar!
Passo 3
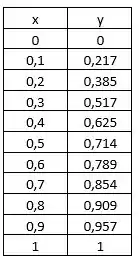
O próximo passo será a construção do gráfico de equilíbrio. Para isso, vamos precisar usar a volatilidade relativa (). Então, vamos escolher vários valores de entre e e , em seguida, vamos calcular os valores de relativos.
Para isso, vamos precisar utilizar a equação que vimos em uns tópicos anteriores:
E aí calculando vamos obter que:
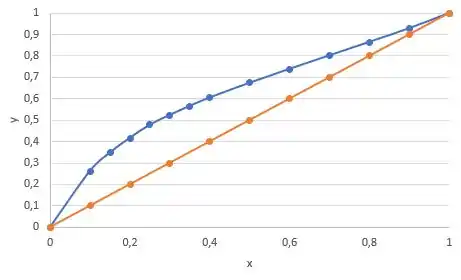
E agora bora plotar esse gráfico lembrando de plotar também a diagonal ( ) 😊
Passo 4
Agora sim, vamos começar o Mc-Cabe Thiele. Nós vamos marcar no gráfico as informações que temos sobre os produtos de topo, fundo, sobre as nossas duas cargas. Para marcar a carga parcialmente vaporizada, precisamos calcular a inclinação da reta .
Sabemos que a inclinação da reta para a carga 1 é dada por:
Onde .
Portanto, a inclinação é
No caso da carga 2, temos um líquido saturado então a nossa reta q é vertical.
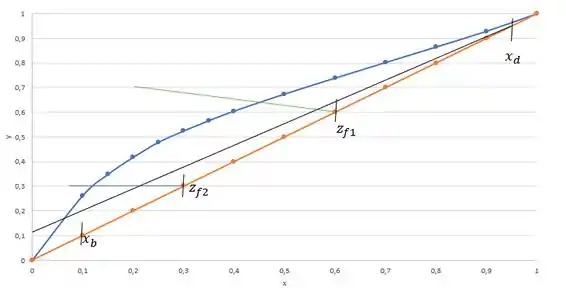
Marcando tudo nosso gráfico, obtemos algo parecido com a imagem abaixo:
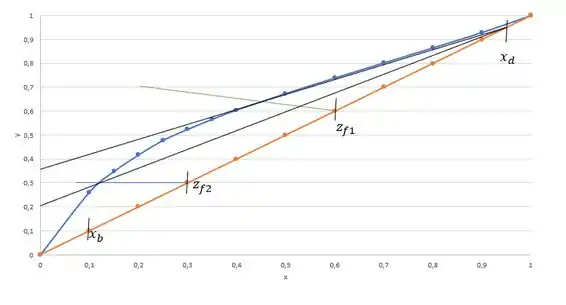
Obs: Se o seu gráfico der um pouquinho diferente, tudo bem! A precisão do papel milimetrado é completamente diferente, então não se fixa muito nos números não. Foca na forma de fazer o exercício, beleza?
Passo 5
Repara que no gráfico fizemos também duas retas forçando pinch. Isso acontece, pois como temos duas cargas, precisamos forçar pinch nas duas, calcular os dois e depois disso escolher o maior deles como o nosso .
O coeficiente linear forçando o pinch na carga 1 é e na carga 2 é . Como , conseguimos calcular as .
Para o caso da carga 1:
Para o caso da carga 2:
Portanto, vamos utilizar a maior entre elas, ou seja, .
E a Razão de Refluxo operacional é vezes a mínima, sendo, portanto, .
Passo 6
Agora, que já temos a podemos calcular o nosso coeficiente linear operacional.
Bora, marcar essa reta?
No entanto, repara que só temos uma reta, mas a nossa coluna possui três seções. Então, precisamos calcular no mínimo mais uma reta, para conseguir determinar as três retas.
Passo 7
Bem, podemos começar fazendo um balanço de massa na envoltória que marcamos aí nesse desenho 😊
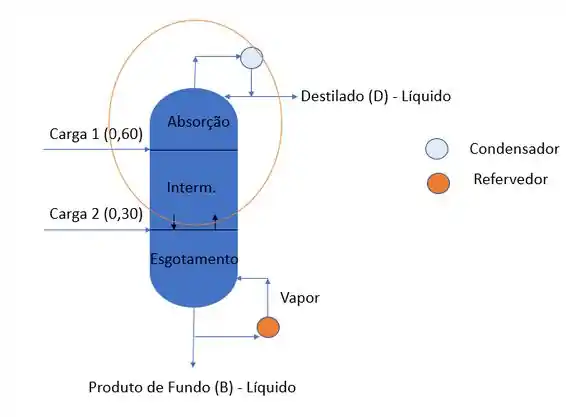
Fazendo esse balanço de Massa, obtemos que:
Onde e são as vazões na seção intermediária.
Com isso, vamos isolar o e deixar nossa equação com o formato parecido com o de uma equação da reta.
Para marcar esse ponto nos eixos do , vamos considerar . Assim, temos que:
No entanto, nós não conhecemos o valor de e precisamos calculá-lo e, portanto, essa será nossa próxima etapa.
Passo 8
corresponde a vazão de vapor da seção intermediária. Portanto, podemos tentar fazer o balanço olhando só para o prato de carga perto dessa seção.
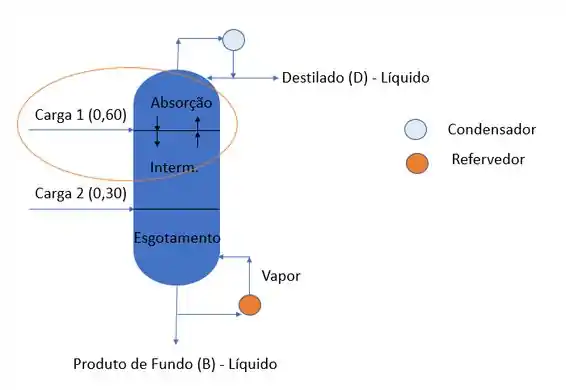
Sabemos que a vazão de vapor que sobe acima do prato de carga é a vazão de vapor antes do prato e a parte da carga que é vapor, portanto é calculado por:
Nós não conhecemos que é a vazão da seção de absorção, mas podemos calcular em função do produto de topo e da razão de refluxo, pois sabemos que:
Portanto, podemos achar agora :
Com isso, conseguimos calcular o , pois:
Logo, a nossa ROSINT vai da interseção da nossa ROSA com a reta até esse ponto que calculamos.
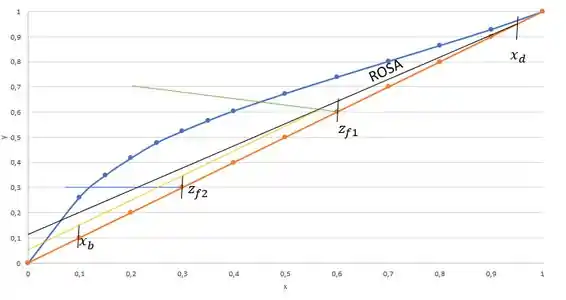
Agora, vamos só fazer uma limpeza no desenho para organizar ele, ok? A ROSA só precisa ser representada até a interseção com a reta e a ROSINT, por sua vez, fica entre as duas cargas.
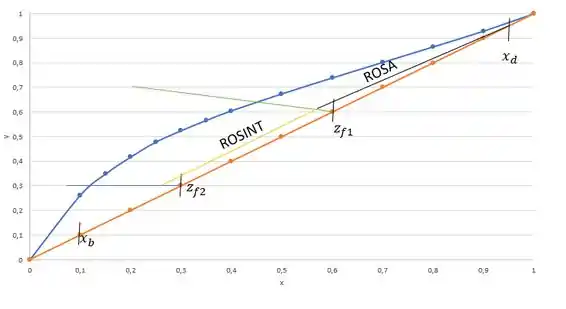
Para traçarmos os estágios falta desenhar a ROSE. A ROSE vai desde o até o encontro da ROSINT com a reta .
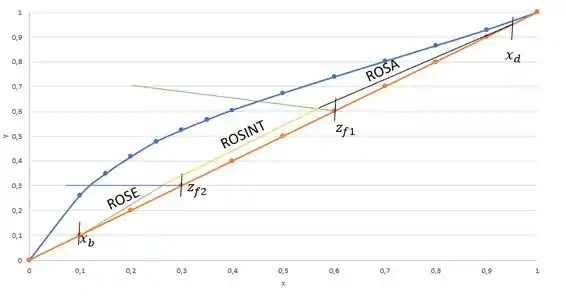
Portanto, agora temos todas as nossas retas de operação traçadas.
Passo 9
Bora traçar os estágios de equilíbrio? Lembrando que sempre que passar da reta , precisamos trocar de reta de operação, beleza?
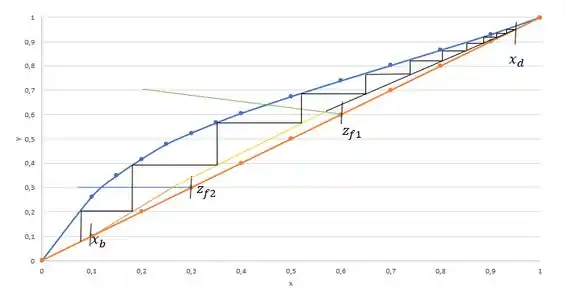
Então, temos 11 estágios, que é o número de vezes que os estágios tocam a curva.
Resposta
11 estágios.