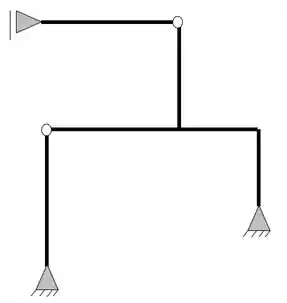
Faça o balanceamento de incógnitas e equações do pórtico abaixo.
Passo 1
Vamos lá então. Sabemos que para solucionar esse tipo de problema precisamos seguir um passo a passo que irá nos ajudar nesse balanceamento, e a sequência de passos é
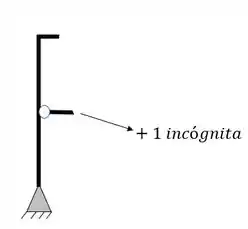
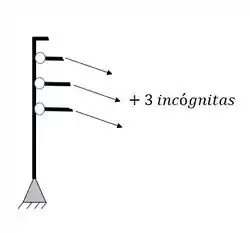
- Primeiro devemos fazer o balanceamento de incógnitas, e sabemos que as incógnitas são dadas pelos apoios ou por tirantes, quando esses últimos existem, e o número de incógnitas é dado da seguinte maneira:
- Em segundo lugar devemos fazer a contagem do número de equações, e ela será feita de duas maneiras, temos as 3 equações de equilíbrio que já conhecemos, e também temos a relação de equações dadas por cada rótula que aparece no nosso pórtico, em que o número de equações é dado pelo número de barras que chegam na nossa rótula, subtraído de um, e com isso podemos ver abaixo como contabilizar as nossas equações
- Por fim fazemos o equilíbrio de equações e incógnitas e verificamos qual o tipo de estruturas que temos, que respeitará uma das seguintes relações
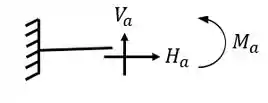
Apoios
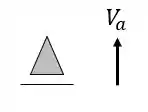
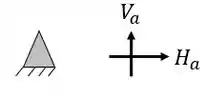
Tirantes
Equações de equilíbrio
Rótulas no pórtico
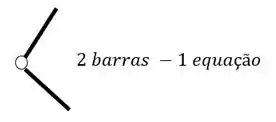
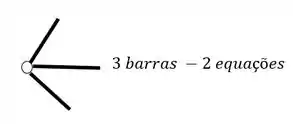
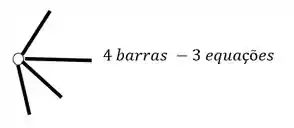
Isostático
E uma reação de apoio em cada direção
Hipostático
Ou não existe uma reação de apoio em cada direção
Hiperestático
E uma reação de apoio em cada direção
Entendido tudo isso, vamos aplicar ao nosso exercício.
Passo 2
Já sabemos que a primeira coisa que devemos fazer é a contabilização do número de incógnitas do nosso problema, olhando a nossa estrutura temos que
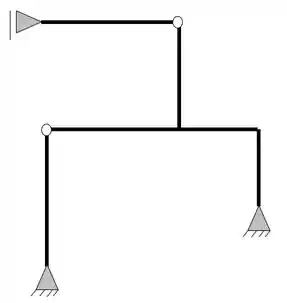
Ela possui um apoio do primeiro gênero (apenas 1 reação) e dois apoios do segundo gênero (2 reações), com isso podemos dizer que as nossas reações de apoios serão
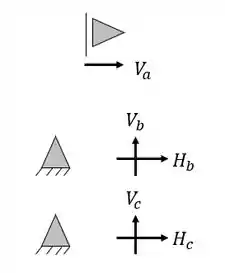
Logo, fazendo a contabilidade, podemos ver que temos ao todo 5 incógnitas no nosso problema, além do mais, não possuímos nenhuma corda ou tirante. Feito isso vamos ao segundo passo.
Passo 3
O segundo passo consiste em contabilizarmos o número de equações. Já sabemos de cara que temos 3 equações de equilíbrio
E que o nosso pórtico apresenta duas rótulas
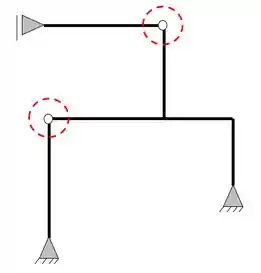
Como podemos ver, temos duas barras nessas rótulas, logo, teremos o seguinte
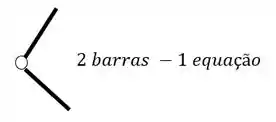
Fazendo a contabilidade, teremos um total de 5 equações, 3 de equilíbrio e 1 de cada rótula.
Passo 4
Agora é simples, basta fazermos o balanceamento.
Nosso pórtico possui 5 incógnitas e 5 equações, logo podemos dizer que
E temos uma reação de apoio em cada direção
Logo a nossa estrutura de pórtico é uma estrutura do tipo isostática.
Resposta
Pórtico isostático com 5 incógnitas e 5 equações