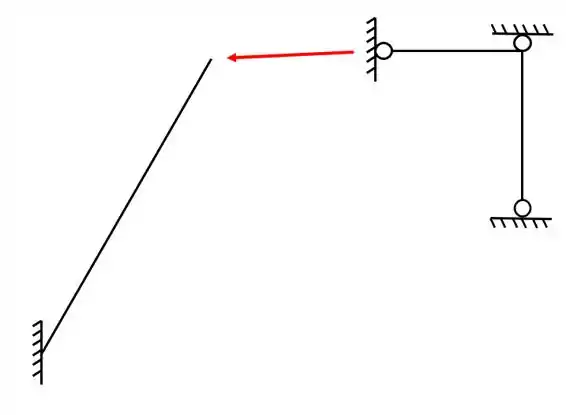
Faça a separação da grelha abaixo em grelhas simples (Lembrar de sempre quebrar nas rótulas)
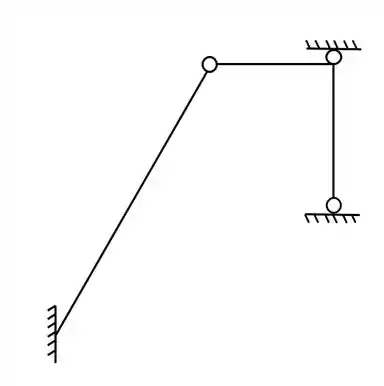
Passo 1
Sabemos que para separarmos a nossa grelha, sempre fazemos o rompimento em um nó com rótula, e depois verificamos se o número de equações (3 de equilíbrio) é compatível com o número de incógnitas (vindas do apoio e que sendo 3 equações de equilíbrio, precisaremos de 3 incógnitas por estrutura). Se o número de equações e de incógnitas for igual, sabemos que teremos feito a separação corretamente, então nosso passo a passo é simples.
- Primeiro achamos as possíveis rótulas a serem rompidas
- Em segundo trocamos a rótula rompida por um apoio fictício
- Por fim verificamos se cada estrutura tem 3 equações de equilíbrio e 3 incógnitas, se bater é porque dividimos certinho.
Vamos aplicar isso ao nosso exercício?
Passo 2
Como vimos primeiro devemos achar as possíveis rótulas a serem rompidas, e no nosso exemplo só temos uma possível rótula a ser rompida, que marcamos aqui em baixo.
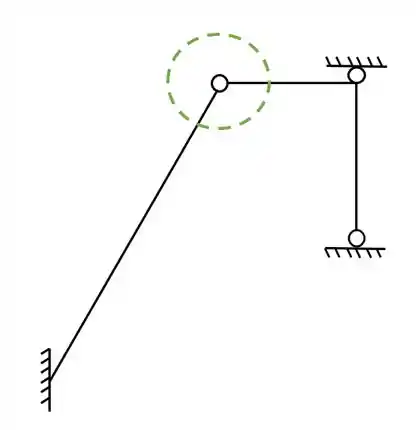
se lembrarmos o que vimos na aula teórica, lembraremos que o rompimento de rótulas gera apoios do primeiro gênero, e o rompimento de dobradiças, geram também, dobradiças.
Porém, vamos ao próximo passo então.
Passo 3
O segundo passo consiste em olharmos a nossa estrutura separada e com o apoio fictício
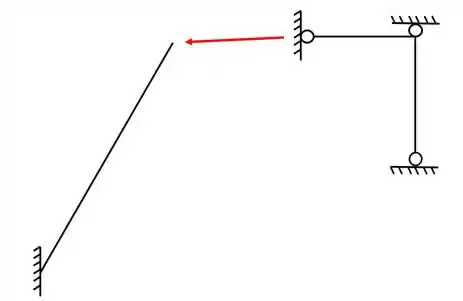
E como podemos ver, de fato se trata de um apoio do primeiro gênero.
Passo 4
Por fim precisamos fazer o balanceamento de equações e incógnitas das nossas estruturas, já sabemos que temos 3 equações de equilíbrio, que serão mais especificadas nas próximas aulas. E quanto aos apoios sabemos que dobradiças geram 2 incógnitas
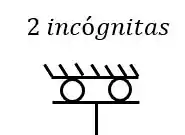
que apoios do primeiro gênero apenas 1 incógnita

E que os engastes geram 3 incógnitas
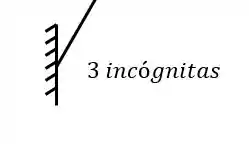
Dessa forma olhando cada estrutura separadamente, teremos que
- Primeira estrutura
- Segunda estrutura
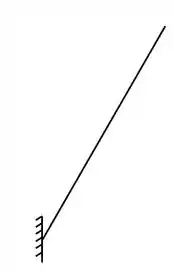
Vemos que ela possui 1 apoio de engaste, ou, do terceiro gênero, logo, possui 3 incógnitas. Como temos 3 incógnitas e 3 equações, sabemos que a nossa estrutura foi dividida corretamente.
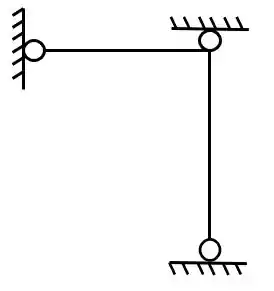
Vemos que ela possui 3 apoios do primeiro gênero, logo, possui 3 incógnitas, já que cada apoio gera uma incógnita. Como temos 3 incógnitas e 3 equações, sabemos que a nossa estrutura foi dividida corretamente.
E dessa forma ao invés de resolvermos uma estrutura muito complexa de grelhas, resolveríamos duas mais simples.
Resposta
A separação da grelha será