Construa a função de transferência abaixo no SIMULINK e compare as respostas ao degrau, com controladores P, PI e PD:
Passo 1
Neste exercício, vamos comparar a resposta ao degrau de uma função de transferência associada a três controladores diferentes: P, PI e PD. Por isso, construiremos três diagramas de blocos, um para cada controlador. Cada diagrama terá os seguintes blocos:
- Um blocos “Step”, representando o degrau unitário;
- Um bloco “Sum” para fechar a malha e calcular o sinal de erro;
- Um bloco “Transfer Fcn”, representando ;
- Um bloco “PID Controller”, representando o controlador do diagrama.
Um bloco “Mux” receberá a saída dos três diagramas e unirá os três sinais em um só, que entrará em um bloco “Scope”. Desta forma, teremos as três saídas representadas em um único gráfico, permitindo sua comparação.
Passo 2
Vamos começar modelando o diagrama que terá o controlador PD. Quando ele estiver concluído, faremos um “copia e cola” dele para gerarmos os outros dois diagramas.
Em um novo modelo, insira um bloco “Step” seguido de um bloco “Sum” e faça com que “Sum” tenha uma entrada positiva e outra negativa. Conecte o bloco “Step” à entrada com o sinal de de “Sum”:
![]()
Agora vamos inserir o bloco que representará o controlador PD. Vá à biblioteca “Continuous”, encontre o bloco “PID Controller”, arraste-o para modelo e conecte sua entrada à saída de “Sum”:

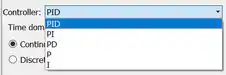
Altere o parâmetro “Controller”, destacado abaixo, de “PID Controller” para que ele vire um controlador PD.

Na lista com várias estruturas pré-programadas de “Controller”, escolha o , de “proporcional”:
Mais embaixo na janela dos parâmetros de “PID Controller”, entramos com o ganho proporcional no campo “Proportional (P)”:
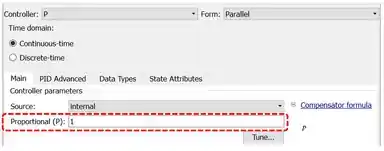
O valor padrão de é , vamos deixar assim. Clique em “OK” pra registrar as mudanças.
Passo 3
Insira um bloco “Transfer Fcn”, que representará , e conecte-o à saída do bloco “PID Controller”:

Entre com alterando os parâmetros “Numerator coefficients” e “Denominator coefficients” do bloco “Transfer Fcn”:

Após definir , insira um bloco “Mux” no modelo, altere seu número de entradas de para e conecte a saída de “Transfer Fcn” à entrada de “Mux” de cima:

Para fechar a malha, clique na entrada negativa de “Sum” e arraste. Aparecerá uma flecha vermelha. Conecte sua “ponta solta” na flecha entre o bloco “Transfer Fcn” e o “Mux”:

Passo 4
Para fazer os diagramas dos controladores PI e PD, selecione os blocos “Sum”, “PID Controller” e “Transfer Fcn” e faça um Ctrl+C Ctrl+V deles duas vezes:
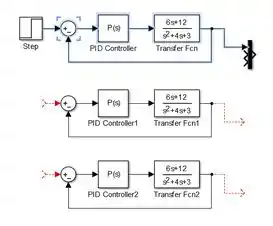
Vamos dar uma rearranjada nos blocos. Primeiramente, conecte o bloco “Step” à entrada positiva dos dois blocos “Sum” novos. Em seguida, conecte as saídas dos dois novos blocos “Transfer Fcn” às entradas restantes de “Mux”:
Passo 5
Vamos transformar os dois novos blocos “PID Controller” em controladores PI e PD. Vamos fazer o diagrama do meio ter o controlador PI. Clique duas vezes sobre o bloco “PID Controller1” para mudar o parâmetro “Controller” para .
Após selecionar em “Controller”, temos os seguintes parâmetros que estabelecem os ganhos do controlador:
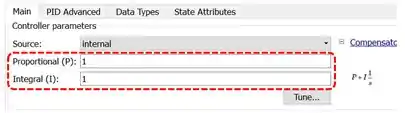
Dessa vez, além do campo “Proportional (P)”, temos o campo “Integral (I)”, onde entramos a constante de integração. Vamos usar seus valores padrão de .
O diagrama de baixo terá o controlador PD. Clique duas vezes sobre o bloco “PID Controller2” e mude o parâmetro “Controller” para . Quando selecionamos em “Controller”, os seguintes parâmetros que definem os ganhos do controlador aparecem:
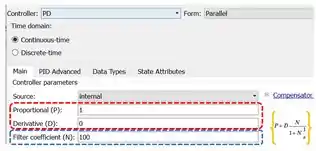
Destacado em vermelho, temos o ganho proporcional e a constante de derivação, correspondendo a “Proportional (P)” e a “Derivative (D)”, respectivamente. Faremos ambos os campos iguais a , por isso, troque o de “Derivative (D)” por .
Destacado em azul, temos o parâmetro “Filter coefficient (N)”, que serve para implementar uma ação derivativa. Quando tem um valor muito alto, a expressão (destacada em amarelo) tende a , correspondendo à parte derivativa da função de transferência de um controlador PD. Vamos usar o valor padrão de .
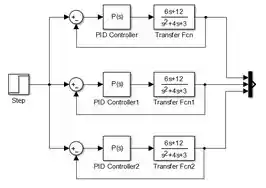
Após ter modelador os controladores PI e PD, seu diagrama deve estar assim:

Repare que o texto dentro dos blocos “PID Controller” correspondem ao controlador que eles modelam. Isso nos ajuda a identificar quem é quem.
Passo 6
Para finalizar o modelo, insira um bloco “Scope” e conecte sua entrada à saída de “Mux”:

Hora de simular e ver os resultados! Rode seu programa e você terá:
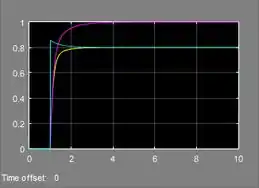
A curva amarela corresponde à resposta de com o controlador P, pois seu diagrama está conectado à entrada de cima de “Mux”.
A curva rosa corresponde ao controlador PI, cujo diagrama está conectado à entrada do meio de “Mux”.
Finalmente, a curva azul piscina corresponde ao controlador PD, pois o diagrama com o PD está conectado à entrada de baixo de “Mux”.
Resposta
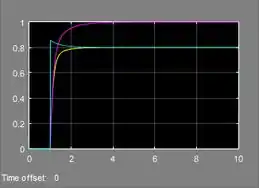
A curva amarela corresponde ao controlador P, com ganho .
A curva rosa corresponde ao controlador PI, com ganhos .
A curva azul piscina corresponde ao controlador PD, com ganhos .