Controle PID no SIMULINK
Produzido por Gustavo BarbosaTeoria
Introdução
E aí, tudo certo? Aviso aos controleiros de plantão que aula de hoje promete! Vamos ver como modelar controladores no SIMULINK!

Mas antes de partirmos para o SIMULINK, vamos dar uma relembrada no porquê de usar controladores e nas estruturas de controle mais utilizadas.
Às vezes acontece de um sistema em malha fechada não apresentar uma resposta legal: pode acontecer de essa resposta ser muito alta ou demorar muuuuito para se estabilizar (ou continuar oscilando para sempre). Nesses casos, usamos controladores para modificar a função de transferência e obter uma resposta satisfatória.
Em um diagrama de blocos, normalmente o controlador fica entre a função de transferência original (também chamada de planta) e o somador em um sistema de malha fechada, como na figura abaixo:
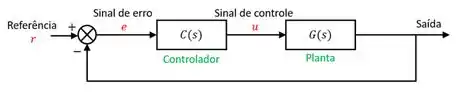
Existem quatro estruturas de controle, cujas características definem a função de transferência do controlador.
A estrutura mais simples é o controlador proporcional, onde o controlador é simplesmente um ganho :
Desta forma, o sinal de controle é dado por . Neste controlador, existe apenas um parâmetro a ser ajustado: o ganho .
No controle proporcional-derivativo (PD), o sinal de controle é proporcional ao erro e à derivada do erro, isto é, depende da variação do erro. Desta forma, a função de transferência do controlador é:
Onde é a constante de derivação. Este controlador é utilizado para melhorar o comportamento transitório do sistema a partir do ajuste de dois parâmetros: e .
O controlador proporcional-integral (PI) tem um sinal de controle proporcional à integral do erro e tem como função de transferência:
Onde é a constante de integração. Os parâmetros ajustáveis deste controlador são e .
Finalmente, um dos controladores mais utilizados na indústria é o controlador proporcional-integral-derivativo (PID), que é soma de três termos: um termo proporcional ao erro, um termo proporcional à integral do erro e um termo proporcional à derivada do erro. Ele tem como função de transferência:
Logo, este controlador tem três parâmetros ajustáveis: , e .
Normalmente esses os parâmetros , e são representados por , e , respectivamente. Aqui eu optei por chamá-los de , e porque é assim que eles são indicados no SIMULINK, como veremos mais pra frente.
Existem alguns métodos para determinar os parâmetros dos controladores, que normalmente são usados como ponto de partida. Em seguida, se necessário, ajustam-se os parâmetros, avaliando se a resposta atende aos requisitos do projeto.
Por isso que é importante saber modelar controladores no SIMULINK, para poder executar esse processo de “tentativa e erro” de ajuste de parâmetros, já que ele faz as simulações pra gente.
Modelando controladores usando vários blocos
Podemos construir controladores P, PI, PD e PID com blocos que já conhecemos do SIMULINK. Digamos que você tenha a planta e queira fazer um controlador para ela:
Podemos fazer um controlador proporcional usando o bloco “Gain”, da biblioteca “Math Operations”. Assumindo , o diagrama de blocos no SIMULINK fica assim (considerando um “Step” como referência e tendo um “Scope” como saída):
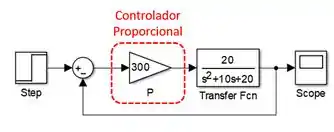
Dica: você pode mudar o texto que tem embaixo dos bloquinhos clicando sobre o texto e digitando. Isso ajuda bastante a não nos perdermos quando trabalhamos com diagramas muito grandes.
Para construir os demais controladores, usamos a operação de blocos em paralelo da álgebra de blocos:
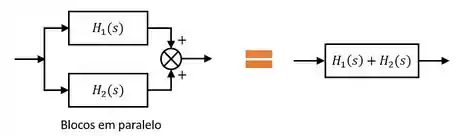
Quando temos dois blocos, com funções de transferência e , sendo somados em paralelo, como na figura acima, podemos substituir essa operação por um único bloco cuja função de transferência é .
Para fazer um controlador PD no SIMULINK, associamos em paralelo um bloco “Gain” para a parte proporcional e, para a parte derivativa, outro bloco “Gain” com a constante de derivação e um bloco “Derivative” da biblioteca “Continuous”:
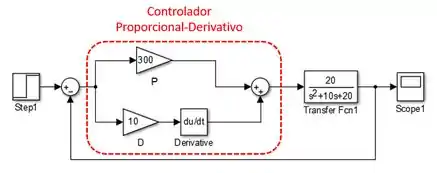
No diagrama acima, assumimos e .
O diagrama de blocos de um controlador PI no SIMULINK é bem parecido com o de cima: associamos em paralelo um bloco “Gain” para a parte proporcional e, para a parte itegrativa, outro bloco “Gain” com a constante de integração e um bloco “Integrator” da biblioteca “Continuous”. Assumindo e :
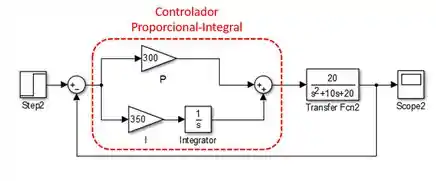
Finalmente, para construir um controlador PID usando vários blocos do SIMULINK, fazemos uma associação em paralelo com os blocos “Gain”, “Derivative” e “Integrator” da seguinte forma:
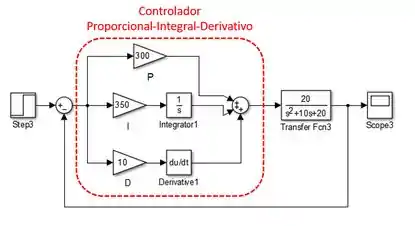
Esta forma de fazer controladores com múltiplos blocos é interessante para entendermos bem como eles funcionam. Mas sabia que o SIMULINK tem um bloco específico para controladores? Desta forma, conseguimos fazer a mesma coisa dos exemplos acima, mas com um único bloco só, deixando nosso modelo bem mais compacto.
Modelando controladores com UM ÚNICO bloco: “PID Controller”
O bloco que modela controladores é o “PID Controller”, da biblioteca “Continuous”:

Ele pode modelar qualquer uma das quatro estruturas de controle que vimos, basta alterar seus parâmetros. Abaixo temos a janela com os parâmetros do bloco “PID Controller”:
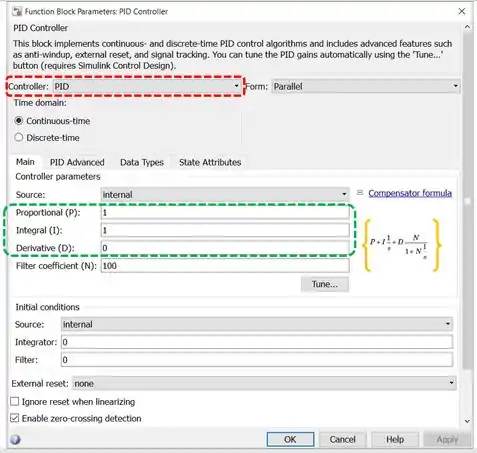
Dá pra ver que ele tem um monte de pârametro, mas na prática alteramos mais as propriedades que estão destacadas. No destaque vermelho, temos o parâmetro “Controller”, que é onde definimos qual estrutura de controle queremos: PID, PI, PD, P ou I.

No campo destacado em verde, ajustamos os parâmetros , e do controlador.
Por padrão, o bloco “PID Controller” modela um controle PID. A função de transferência do controlador é mostrada na região destacada pelos colchetes amarelos.
“Ué, mas a parte derivativa da função de transferência tá diferente do que a gente viu!”, você deve estar pensando. Vimos que a parte derivativa do PID é e ali temos:
O que é esse ? é um parâmetro chamado “filter coefficient” e é utilizado para implementar uma ação derivativa. Precisamos desse porque uma função de transferência do tipo é dita imprópria: o grau do polinômio do numerador () é maior do que o grau do polinômio do denominador (). Em uma função de transferência tem que ser o contrário: a ordem do denominador tem que ser maior do que a ordem do numerador.
O serve para contornar essa restrição. Quando é bem grande, a expressão tende a .
Vamos implementar o mesmo controle PID que fizemos na seção anterior. Vamos substituir aqueles três blocos em paralelo por um único bloco:

Bem mais compacto! Vamos alterar as propriedades do bloco “PID Controller”, alterando os parâmetros , e para os mesmos valores que usamos na seção anterior. Eles ficarão assim:
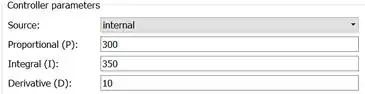
Podemos comparar as respostas do sistema quando utilizamos vários blocos para construir um controlador PID e quando usamos somente o bloco “PID Controller”, unindo os diagrams por um bloco “Mux”:
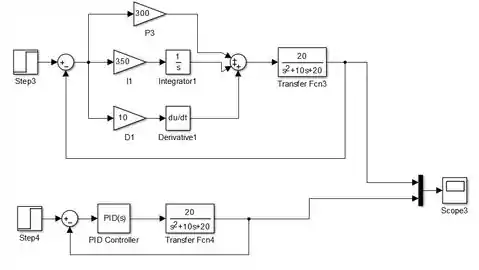
Abaixo temos o gráfico com as respostas: em amarelo, é a resposta do sistema com o controle PID feito de vários blocos. Em rosa, é a resposta com o bloco “PID Controller”.
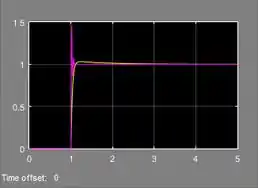
Note que as respostas são ligeiramente diferentes. Um dos motivos dessa diferença é o “filter coefficient”: se aumentarmos , a ação derivativa de “PID Controller” ficará mais próxima do controlador com os blocos em paralelo. O bloco “PID Controller” tem outras propriedades que também impactam a resposta e que levam a essa diferença entre as curvas.
E aí? Curtiu a aula de hoje?
Não esqueça de fazer os exercícios para fixar bem o conteúdo ;D
Modelando controladores usando vários blocos
Modelando controladores com UM ÚNICO bloco: “PID Controller”
Exercícios Resolvidos
Exercício Resolvido #1
“Adaptado de USP e Texas A&M University - Simulink and block diagram – 2016 Brazil Study Abroad Program. Hands On! (2016)”
Construa a função de transferência abaixo no SIMULINK e compare as respostas ao degrau, com controladores P, PI e PD:
Passo 1
Neste exercício, vamos comparar a resposta ao degrau de uma função de transferência associada a três controladores diferentes: P, PI e PD. Por isso, construiremos três diagramas de blocos, um para cada controlador. Cada diagrama terá os seguintes blocos:
- Um blocos “Step”, representando o degrau unitário;
- Um bloco “Sum” para fechar a malha e calcular o sinal de erro;
- Um bloco “Transfer Fcn”, representando ;
- Um bloco “PID Controller”, representando o controlador do diagrama.
Um bloco “Mux” receberá a saída dos três diagramas e unirá os três sinais em um só, que entrará em um bloco “Scope”. Desta forma, teremos as três saídas representadas em um único gráfico, permitindo sua comparação.
Passo 2
Vamos começar modelando o diagrama que terá o controlador PD. Quando ele estiver concluído, faremos um “copia e cola” dele para gerarmos os outros dois diagramas.
Em um novo modelo, insira um bloco “Step” seguido de um bloco “Sum” e faça com que “Sum” tenha uma entrada positiva e outra negativa. Conecte o bloco “Step” à entrada com o sinal de de “Sum”:
![]()
Agora vamos inserir o bloco que representará o controlador PD. Vá à biblioteca “Continuous”, encontre o bloco “PID Controller”, arraste-o para modelo e conecte sua entrada à saída de “Sum”:

Altere o parâmetro “Controller”, destacado abaixo, de “PID Controller” para que ele vire um controlador PD.

Na lista com várias estruturas pré-programadas de “Controller”, escolha o , de “proporcional”:
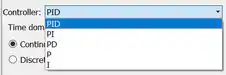
Mais embaixo na janela dos parâmetros de “PID Controller”, entramos com o ganho proporcional no campo “Proportional (P)”:
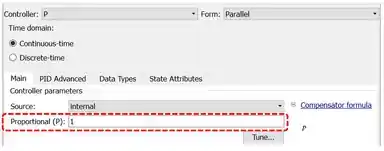
O valor padrão de é , vamos deixar assim. Clique em “OK” pra registrar as mudanças.
Passo 3
Insira um bloco “Transfer Fcn”, que representará , e conecte-o à saída do bloco “PID Controller”:

Entre com alterando os parâmetros “Numerator coefficients” e “Denominator coefficients” do bloco “Transfer Fcn”:

Após definir , insira um bloco “Mux” no modelo, altere seu número de entradas de para e conecte a saída de “Transfer Fcn” à entrada de “Mux” de cima:

Para fechar a malha, clique na entrada negativa de “Sum” e arraste. Aparecerá uma flecha vermelha. Conecte sua “ponta solta” na flecha entre o bloco “Transfer Fcn” e o “Mux”:

Passo 4
Para fazer os diagramas dos controladores PI e PD, selecione os blocos “Sum”, “PID Controller” e “Transfer Fcn” e faça um Ctrl+C Ctrl+V deles duas vezes:
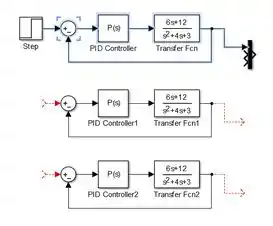
Vamos dar uma rearranjada nos blocos. Primeiramente, conecte o bloco “Step” à entrada positiva dos dois blocos “Sum” novos. Em seguida, conecte as saídas dos dois novos blocos “Transfer Fcn” às entradas restantes de “Mux”:
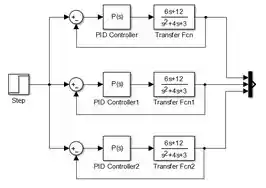
Passo 5
Vamos transformar os dois novos blocos “PID Controller” em controladores PI e PD. Vamos fazer o diagrama do meio ter o controlador PI. Clique duas vezes sobre o bloco “PID Controller1” para mudar o parâmetro “Controller” para .
Após selecionar em “Controller”, temos os seguintes parâmetros que estabelecem os ganhos do controlador:
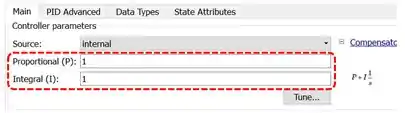
Dessa vez, além do campo “Proportional (P)”, temos o campo “Integral (I)”, onde entramos a constante de integração. Vamos usar seus valores padrão de .
O diagrama de baixo terá o controlador PD. Clique duas vezes sobre o bloco “PID Controller2” e mude o parâmetro “Controller” para . Quando selecionamos em “Controller”, os seguintes parâmetros que definem os ganhos do controlador aparecem:
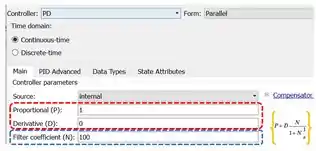
Destacado em vermelho, temos o ganho proporcional e a constante de derivação, correspondendo a “Proportional (P)” e a “Derivative (D)”, respectivamente. Faremos ambos os campos iguais a , por isso, troque o de “Derivative (D)” por .
Destacado em azul, temos o parâmetro “Filter coefficient (N)”, que serve para implementar uma ação derivativa. Quando tem um valor muito alto, a expressão (destacada em amarelo) tende a , correspondendo à parte derivativa da função de transferência de um controlador PD. Vamos usar o valor padrão de .
Após ter modelador os controladores PI e PD, seu diagrama deve estar assim:

Repare que o texto dentro dos blocos “PID Controller” correspondem ao controlador que eles modelam. Isso nos ajuda a identificar quem é quem.
Passo 6
Para finalizar o modelo, insira um bloco “Scope” e conecte sua entrada à saída de “Mux”:

Hora de simular e ver os resultados! Rode seu programa e você terá:
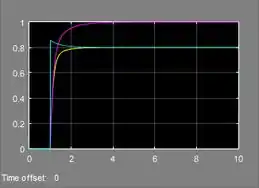
A curva amarela corresponde à resposta de com o controlador P, pois seu diagrama está conectado à entrada de cima de “Mux”.
A curva rosa corresponde ao controlador PI, cujo diagrama está conectado à entrada do meio de “Mux”.
Finalmente, a curva azul piscina corresponde ao controlador PD, pois o diagrama com o PD está conectado à entrada de baixo de “Mux”.
Resposta
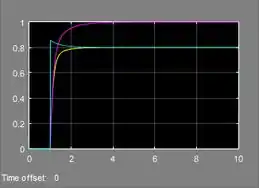
A curva amarela corresponde ao controlador P, com ganho .
A curva rosa corresponde ao controlador PI, com ganhos .
A curva azul piscina corresponde ao controlador PD, com ganhos .