Conforme mostrado na Fig. P2.47, a parede externa de um edifício tem de espessura e possui uma condutividade térmica média de . Em regime permanente, a temperatura da parede diminui linearmente de na superfície interna para na superfície externa. A temperatura externa relativa ao ambiente é e o coeficiente de transferência de calor por convecção é . Determine
- a temperatura em , e
- a taxa de transferência de calor através da parede, em por de área de superfície.
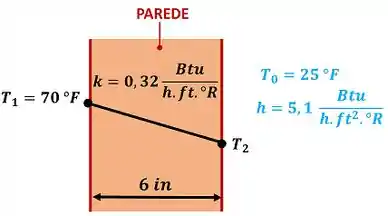
Passo 1
Oi, querid@s! Blz?

Então, esse é um exercício que mistura convecção com condução. Nessa questão, a parede conduz calor da superfície esquerda pra superfície direita a uma taxa . Ao chegar na superfície direita, o calor é perdido pro ar por convecção na mesma taxa .
Primeiro, o enunciado quer saber a temperatura da superfície direita.
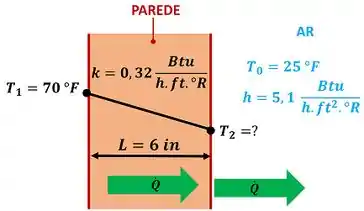
é a temperatura da superfície esquerda, é a condutividade térmica da parede, é o coeficiente de transferência de calor por convecção e é a temperatura do ar.
Com esses dados em mão, somos capazes de achar . Pra isso, usaremos duas equações no próximo passo: a lei de Fourier e a lei de resfriamento de Newton.
Passo 2
Nesse passo, calcularemos o valor de e resolveremos a letra (a) da questão. Pra isso calcularemos o valor da taxa de calor trocada através da parede de duas formas. A primeira será através da lei de Fourier abaixo que calcula pra condução.
onde é a diferença de temperatura entre os dois lados da parede e é a área da parede. Ou seja:
A outra forma de se calcular é através da lei de resfriamento de Newton abaixo.
Nós podemos igualar as duas equações de , porque o enunciado diz que o problema está em regime permanente. Isso significa que toda taxa de calor que entra em um lado da parede por condução, deve sair por esse lado através da convecção. Igualando essas equações, conseguimos achar uma fórmula pra .
Antes de substituir os dados na equação precisamos converter de pra , dividindo por . Além disso, precisamos converter e para grau Rankine, somando essas e com .
Diminuindo de , achamos o valor de em que a letra (a) pediu.
Agora que temos o resultado da letra (a), podemos partir pra letra (b).
Passo 3
A letra (b) da questão quer saber quanto vale a taxa de transferência de calor que a parede conduz, dividida pela área da parede. Ou seja,, a questão quer saber agora quanto vale . Podemos fazer esse cálculo tanto pela lei de Fourier quanto pela lei de resfriamento de Newton. Escolhemos então, sem nenhum motivo especial, a segunda opção:
Aeeee! Essa foi a letra (b) da questão! Bem mais rápida, né?