Convecção
Teoria
Relembrando a condução de calor e a lei de Fourier
Quando estudamos transferência de calor por condução, nós descobrimos que o calor pode passar de um objeto para outro através do choque entre as moléculas desses objetos. Para visualizar isso melhor, podemos imaginar um termômetro medindo a nossa temperatura. Como o calor passa do corpo quente pro termômetro frio para fazer o mercúrio se dilatar?
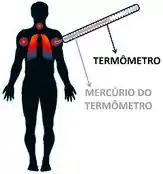
Isso acontece, porque as moléculas do corpo estão mais agitadas e se chocam com as moléculas do termômetro. Isso faz o termômetro esquentar. Nesse caso, o calor caminha do corpo para o termômetro, mas tanto o corpo quanto o termômetro ficam parados durante esse processo. Apenas as moléculas do corpo e do termômetro se movimentam e se chocam.
Esse processo, no qual o calor passa de um objeto parado para outro objeto parado por causa do contato físico entre os dois, é chamado de transferência de calor por condução! A taxa de calor que passa do corpo para o termômetro pode ser calculada pela fórmula chamada de lei de Fourier. Essa fórmula se encontra abaixo.
onde é a condutividade térmica do material que compõe o objeto, é a área da superfície onde ocorre a transferência de energia e é a derivada da temperatura em relação a uma direção .
O que é a convecção?
Nem sempre a transferência de calor ocorre por condução. Existem vários casos que os objetos que trocam calor NÃO estão parados! Por exemplo, quando estamos com febre e queremos abaixar nossa temperatura, tomamos um banho mais frio. Nesse caso, o corpo parado troca calor com a água em movimento. Como chamamos esse processo?
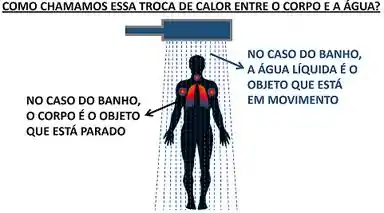
O processo de troca de calor entre uma superfície sólida e um fluido (líquido, vapor e gás) em movimento é chamado de convecção! A convecção é uma combinação da condução de calor com o movimento do fluido. No banho, a água rouba o calor do corpo por condução (choque entre moléculas do corpo e da água) e depois carrega esse calor para longe ao se movimentar!
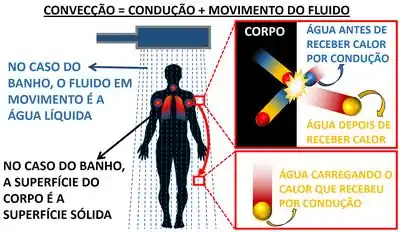
Nós vimos que a lei de Fourier é usada para calcular a taxa de calor trocada por condução. Mas se a condução faz parte da troca de calor por convecção, podemos usar a lei de Fourier para calcular a taxa de calor trocada por convecção também?
NÃO! Usaremos outra fórmula para calcular a taxa de calor trocada por convecção!
A lei do resfriamento de Newton
A fórmula para o cálculo da taxa de transferência de calor por convecção é chamada de lei do resfriamento de Newton. Ela se encontra abaixo.
onde:
- é o coeficiente de transferência de calor por convecção. Quanto maior esse valor, mais calor a superfície troca com o fluido. Sua unidade no Sistema Internacional (S.I.) é o watt por metro quadrado e por kelvin . ATENÇÃO! Não confunda esse coeficiente com a entalpia específica ! Os dois são totalmente diferentes!
- é a área da superfície, onde a transferência de calor ocorre. Ela é medida em metro quadrado segundo o Sistema Internacional (S.I.);
- é a temperatura da superfície sólida. Ela é medida em grau Celsius ou em kelvin segundo o Sistema Internacional (S.I.);
- é a temperatura do fluido. Ela é medida em grau Celsius ou em kelvin segundo o Sistema Internacional (S.I.). e estar na mesma unidade!
- é a taxa de transferência de calor entre a superfície sólida e o fluido em movimento. Sua unidade no Sistema Internacional (S.I.) é o watt . O seu valor é sempre positivo! Para descobrir o sentido do calor, basta saber qual temperatura é maior: ou . Se for maior que , o calor sai do fluido e vai para a superfície sólida a uma taxa . Se for maior que , o calor sai da superfície sólida e vai para o fluido a uma taxa .
O termo dessa fórmula é o valor da diferença de temperatura sem o sinal! Por exemplo, imagine um bloco de metal frio a sendo esquentado por uma corrente de água quente a . Nesse caso a superfície sólida seria a superfície fria do metal a . O fluido em movimento seria a água quente a .
A diferença entre essas duas temperaturas seria igual a:
Nós não substituiremos por na fórmula! Nós substituiremos pelo valor da diferença sem o sinal! Isso quer dizer que vale:
Por isso:
Agora vamos aprender a usar essa fórmula de cálculo de da convecção, resolvendo um exemplo!
Como saber se o exercício é de condução ou convecção
Uma pessoa com febre decide tomar um banho para abaixar a temperatura do seu corpo que está a . A água do banho se encontra a . A área da superfície do corpo em contato com a água mede . Considerando que o coeficiente de transferência de calor por convecção desse processo vale , calcule a taxa de calor que o corpo perde no banho.
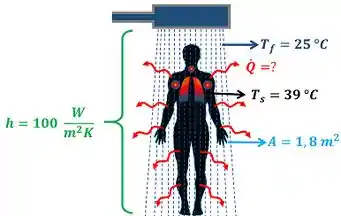
O primeiro passo para resolver esse exercício é saber diferenciar se o exercício é de condução ou convecção! Como podemos descobrir isso? Os enunciados desses dois tipos de exercício são muito parecidos! Os dois informam os valores de pelo menos duas temperaturas e uma área de troca de calor. Então como podemos diferenciar os dois?
A maior diferença entre esses dois enunciados está nos coeficientes que eles dão pra gente! Em exercícios de condução, o enunciado informa a condutividade térmica do material . Já em exercícios de convecção, o enunciado informa o coeficiente de transferência de calor por convecção !
Como o exemplo informou o coeficiente de transferência de calor por convecção, ele é um exemplo de convecção! Isso quer dizer que para calcular a taxa de troca de calor pedida pelo exercício, vamos ter que usar a lei do resfriamento de Newton. Agora que sabemos disso, vamos começar a fazer as contas!
Cálculo da taxa de transferência de calor por convecção
A lei do resfriamento de Newton se encontra abaixo.
Segundo o enunciado, o coeficiente de transferência de calor por convecção desse processo vale .
é a temperatura da superfície sólida. Como a superfície sólida desse exercício é a superfície corpo da pessoa em febre, vale .
é a temperatura do fluido em movimento. Nesse caso, o fluido em movimento é a água líquida que cai do chuveiro e entra em contato com o corpo. Por isso, vale:
O da fórmula é a área da superfície, onde a transferência de calor ocorre. No caso desse exemplo, a área onde ocorre a troca de calor é a área da superfície do corpo que fica em contato com a água. Ela mede segundo a questão!
Substituindo esses valores na fórmula, descobrimos o valor de .
Agora só falta saber qual é o sentido do calor que é trocado entre o corpo e a água!
Para isso, basta ver quem tem a maior temperatura. Como, nesse caso, a superfície sólida tem uma temperatura maior que o fluido, o calor sai do sólido e vai pro fluido!
Como calcular a área A da fórmula
Nem sempre o enunciado do problema informa diretamente o valor da área , onde a troca de calor por convecção ocorre! As vezes somos nós que precisamos calcular esse valor.
Imagine dois casos de troca de calor por convecção. E em um caso, o vento frio passa por cima de uma placa de metal quente. Em outro caso, o vento passa esfria uma esfera de metal.
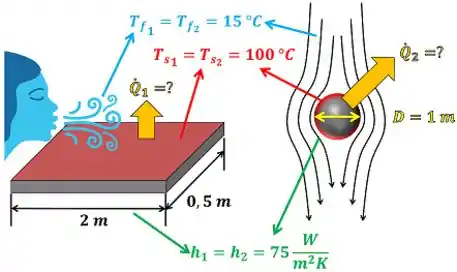
Calcule as áreas de trocas térmicas dos dois casos, usando as dimensões informadas pela figura acima. Determine também a taxa de calor trocada entre a placa e o vento e a taxa de calor trocada entre a esfera e o vento .
No primeiro caso, o vento a passa apenas pela superfície de cima da placa a . Isso significa que a área onde a troca de calor acontece é apenas a área da superfície de cima da placa.
Logo, a taxa de troca de calor entre o vento e a placa vale:
No segundo caso, o vento a passa por toda a superfície a da esfera . Isso significa que a área é igual à área total da esfera de diâmetro igual à
Logo, a taxa de troca de calor entre o vento e a esfera vale:
Depois de ler tanta teoria, vamos exercitar mais esse conhecimento, resolvendo mais exercícios!
A lei do resfriamento de Newton
Como saber se o exercício é de condução ou convecção
Cálculo da taxa de transferência de calor por convecção Q ˙
Como calcular a área A da fórmula
Exercícios Resolvidos
Exercício Resolvido #1
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 96-4.98
Um automóvel percorre uma estrada num dia em que a temperatura ambiente é . A temperatura externa do para-brisa é mantida a pelo escoamento de ar quente na superfície interna do para-brisa. Admitindo que a área do para-brisa é e que o coeficiente de transferência de calor por convecção na superfície externa do para-brisa é , determine a taxa de transferência de calor para o ambiente externo através do para-brisa.
Passo 1
Fala, minha gente! Prontos para exercitar a teoria com essa questão de convecção?
Essa questão quer saber quanto vale a taxa de calor que atravessa o para-brisa do carro por causa da convecção do ar gelado sobre o vidro quente. Como se trata de uma questão de convecção, podemos calcular essa taxa de calor através da lei de resfriamento de Newton.
onde é a área do para-brisa, é a temperatura da superfície que está sendo resfriada, é a temperatura do fluido que está recebendo calor e é o coeficente de transferência de calor por convecção.
A imagem abaixo mostra quando cada termo vale.
Com esses dados em mãos, podemos partir pro cálculo de no próximo passo.
Passo 2
Para achar , basta substituir as informações que temos na equação que temos:
Aeeee! Concluímos a questão!
Resposta
Exercício Resolvido #2
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 104-2-104
Ar quente a é soprado sobre uma superfície plana de a . Considerando que o coeficiente de transferência de calor por convecção é de , determine a taxa de transferência de calor do ar para a placa em .
Passo 1
Oie, pessoal! Estão com energia para exercitar a teoria com essa questão de convecção?
Podemos ver que essa questão de troca de calor é uma questão de convecção, porque o enunciado nos informa o valor do coeficiente de transferência de calor por convecção .
Sempre que o enunciado fala o valor de , a questão envolve troca de calor por convecção!
Essa questão quer saber quanto vale a taxa de calor que a superfície plana recebe do ar quente por causa da convecção. Como se trata de uma questão de convecção, podemos calcular essa taxa de calor através da lei de resfriamento de Newton.
onde é a área da superfície que troca calor, é a temperatura da superfície, é a temperatura do fluido que está trocando calor (no caso é o ar quente).
A imagem abaixo mostra quando cada termo vale.
Com esses dados em mãos, podemos partir pro cálculo de no próximo passo.
Passo 2
Para achar , basta substituir as informações que temos na equação que temos. No entanto, ainda não calculamos quanto vale a área da superfície de troca de calor. Para isso, basta multiplicar as dimensões da superfície presente na figura.
Substituindo os dados na fórmula de :
Mas calma que a questão ainda não terminou! O exercício pediu pra gente calcular a taxa de troca de calor em .
Pra converter de pra , dividimos por .
Agoooora sim concluímos a questão! Bate aqui!
Resposta
Exercício Resolvido #3
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 97-4.100
A área total de transferência de calor do condensador de uma geladeira doméstica é igual a . A temperatura da superfície externa do condensador é e o coeficiente médio de transferência de calor na superfície externa do condensador é igual a . Qual é a quantidade de calor transferida do condensador para o ambiente durante minutos de operação da geladeira.
Passo 1
E aí, galera! Está com energia para exercitar a teoria com essa questão de convecção?
Antes de começar o exercício é necessário ressaltar que o enunciado está incompleto. Faltou ele dizer que a temperatura do ar que está ao redor do condensador vale .
Essa questão quer saber quanto vale o calor que o condensador da geladeira libera para o ambiente durante os minutos que ela fica ligada. Para calcular o valor de precisamos lembrar que a taxa de calor é o calor que o condensador libera a cada segundo. Logo, é a quantidade de segundos que a geladeira fica ligada multiplicada por .
é a taxa de calor que o condensador libera por conta da convecção. Como se trata de uma questão de convecção, podemos calcular essa taxa de calor através da lei de resfriamento de Newton.
onde é a área de do condensador, é a temperatura da superfície que está sendo resfriada (temperatura da superfície do condensador), é a temperatura do fluido que está recebendo calor (temperatura do ar a ) e é o coeficente de transferência de calor por convecção que vale . Com esses dados, achamos no passo seguinte!
Passo 2
Pra ficar mais claro o que cada dado significa e o que precisamos calcular, as informações do enunciado estão organizadas na figura abaixo. Depois de ver a figura podemos partir pra resolução.
Para achar , basta substituir as informações que temos na equação que temos:
Antes de substituir na equação de , precisamos converter de minuto pra segundo, multiplicando por !
Aeeee! Ponto pra gente! Concluímos a questão!
Resposta
Exercício Resolvido #4
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 105-2-108
Um tubo a que conduz água quente possui de diâmetro externo e de comprimento, e perde calor para o ar da vizinhança a por convecção natural. Seu coeficiente de transferência de calor é de . Determine a taxa em com a qual o tubo perde calor por convecção natural.
Passo 1
Oie, pessoal! Bora exercitar a teoria com essa questão de convecção pra tirar 10 na prova?
Essa questão quer saber quanto vale a taxa de calor que o tubo que conduz água perde pro ar frio por causa da convecção. Como se trata de uma questão de convecção, podemos calcular essa taxa de calor através da lei de resfriamento de Newton.
onde é a área da superfície que troca calor (superfície externa do tubo), é a temperatura da superfície externa do tubo, é a temperatura do fluido que está trocando calor (no caso é o ar frio).
A imagem abaixo mostra quando cada termo vale.
Com esses dados em mãos, podemos partir pro cálculo de no próximo passo.
Passo 2
Para achar , basta substituir as informações que temos na equação que temos. No entanto, ainda não calculamos quanto vale a área da superfície externa do tubo. Para isso, usamos a equação da superfície de um cilindro. Mas antes de usar a equação, temos que converter o diâmetro de pra , dividindo por .
Substituindo os dados na fórmula de :
Mas calma que a questão ainda não terminou! O exercício pediu pra gente calcular a taxa de troca de calor em .
Pra converter de pra , dividimos por .
Agoooora sim concluímos a questão! Toca aqui!
Resposta
Exercício Resolvido #5
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 108-2-141
Uma resistência elétrica do tipo fio metálico com de comprimento e diâmetro de submersa em água é usada para determinar experimentalmente o coeficiente de transferência de calor na ebulição da água a . A temperatura da superfície do fio é de quando um amperímetro indica um consumo de potência elétrica de . Assim, o coeficiente de transferência de calor é
Passo 1
E aí, gente! Vamos exercitar a teoria com essa questão de convecção pra arrasar na prova?
Essa questão quer saber quanto vale o coeficiente de transferência de calor por convecção da troca de calor entre a resistência elétrica e a água. Como se trata de uma questão de convecção, podemos calcular através da lei de resfriamento de Newton.
onde é a área da superfície que troca calor (superfície externa do tubo), é a temperatura da superfície externa do tubo, é a temperatura do fluido que está trocando calor (no caso é a água em ebulição a ) e é a potência dissipada pela resistência.
A imagem abaixo mostra quando cada termo vale.
Com esses dados em mãos, podemos partir pro cálculo de no próximo passo.
Passo 2
Para achar , basta substituir as informações que temos na equação que temos. No entanto, ainda não calculamos quanto vale a área da superfície externa do tubo. Para isso, usamos a equação da superfície de um cilindro. Mas antes de usar a equação, temos que converter o diâmetro e o comprimento de pra , dividindo e por .
Além disso, precisamos converter a potência dissipada de pra , multiplicando ela por
Substituindo os dados na fórmula de :
Achamos ! A opção certa é a letra (a)! Pode marcar sem medo!
Resposta
Exercício Resolvido #6
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 97-4.102
A lona e a panela do freio de um automóvel absorvem continuamente durante a frenagem. Admita que a área da superfície externa e que o coeficiente de transferência de calor neste local sejam iguais a e . Sabendo que a temperatura do ar externo é , determine as temperatura externas da lona e da panela do freio nas condições de regime permanente.
Passo 1
Fala, galera! Partiu firmar nosso conhecimento com essa questão de convecção?
Essa questão quer saber quanto vale a temperatura da superfície quente do freio. Para isso, o problema supõe que a taxa de calor que o freio recebe é igual à taxa de calor que o ferio perde para o ar através de convecção. Os dados que temos pra achar estão na figura.
é a área da superfície que troca calor (superfície do freio) e é a temperatura do fluido que está trocando calor (no caso é o ar frio).
Como se trata de uma questão de convecção, podemos calcular a temperatura da superfície do freio através da lei de resfriamento de Newton.
Com esses dados em mãos, podemos partir pro cálculo de no próximo passo.
Passo 2
Para achar , basta substituir as informações que temos na equação que temos.
Uhuuuuuul! Show of ball (show de bola)! Achamos o que o enunciado queria!
Resposta
Exercício Resolvido #7
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 97-4.101
A lâmpada de iluminação interna de uma geladeira permanece acesa apesar da porta estar fechada e a transferência de calor do ambiente para o espaço refrigerado é igual a devido a problemas existentes no isolamento da geladeira. Estas duas transferência de calor podem ser encaradas como “vazamentos” de calor para a geladeira. A área total de transferência de calor do condensador dessa geladeira é e o coeficiente de transferência de calor por convecção na superfície externa do condensador é . Determine a diferença entre a temperatura da superfície externa do condensador e a temperatura ambiente de modo que seja possível transferir para o ambiente o calor que está “vazando” para a geladeira. Admita que a temperatura ambiente seja igual a .
Passo 1
Fala, gente! Partiu fazer um exercício de convecção pra gravar bem a matéria?
Essa questão quer saber quanto vale a diferença de temperatura que faz o condensador de geladeira rejeitar uma taxa de calor igual à taxa de calor que a geladeira recebe através de dois vazamentos (um de e outro de ). Os dados que temos pra achar estão na figura.
é a área da superfície que troca calor (superfície do condensador) e é a temperatura do fluido que está trocando calor (no caso é o ar frio).
Como se trata de uma questão de convecção, podemos calcular a diferença de temperatura entre o condensador e o ar através da lei de resfriamento de Newton.
Com esses dados em mãos, podemos partir pro cálculo de no próximo passo.
Passo 2
Para achar , basta substituir as informações que temos na equação que temos.
Aeeeeeeee! Que tranquilo! Já achamos o que o enunciado queria!
Resposta
Exercício Resolvido #8
Michael J. Moran, Howard N. Shapiro, Daisie D. Boettner e Margaret B. Bailey, Princípios de Termodinâmica para Engenharia, 8ª ed. Rio de Janeiro: LTC, 2018, pp. 67-2.47
Conforme mostrado na Fig. P2.47, a parede externa de um edifício tem de espessura e possui uma condutividade térmica média de . Em regime permanente, a temperatura da parede diminui linearmente de na superfície interna para na superfície externa. A temperatura externa relativa ao ambiente é e o coeficiente de transferência de calor por convecção é . Determine
- a temperatura em , e
- a taxa de transferência de calor através da parede, em por de área de superfície.
Passo 1
Oi, querid@s! Blz?
Então, esse é um exercício que mistura convecção com condução. Nessa questão, a parede conduz calor da superfície esquerda pra superfície direita a uma taxa . Ao chegar na superfície direita, o calor é perdido pro ar por convecção na mesma taxa .
Primeiro, o enunciado quer saber a temperatura da superfície direita.
é a temperatura da superfície esquerda, é a condutividade térmica da parede, é o coeficiente de transferência de calor por convecção e é a temperatura do ar.
Com esses dados em mão, somos capazes de achar . Pra isso, usaremos duas equações no próximo passo: a lei de Fourier e a lei de resfriamento de Newton.
Passo 2
Nesse passo, calcularemos o valor de e resolveremos a letra (a) da questão. Pra isso calcularemos o valor da taxa de calor trocada através da parede de duas formas. A primeira será através da lei de Fourier abaixo que calcula pra condução.
onde é a diferença de temperatura entre os dois lados da parede e é a área da parede. Ou seja:
A outra forma de se calcular é através da lei de resfriamento de Newton abaixo.
Nós podemos igualar as duas equações de , porque o enunciado diz que o problema está em regime permanente. Isso significa que toda taxa de calor que entra em um lado da parede por condução, deve sair por esse lado através da convecção. Igualando essas equações, conseguimos achar uma fórmula pra .
Antes de substituir os dados na equação precisamos converter de pra , dividindo por . Além disso, precisamos converter e para grau Rankine, somando essas e com .
Diminuindo de , achamos o valor de em que a letra (a) pediu.
Agora que temos o resultado da letra (a), podemos partir pra letra (b).
Passo 3
A letra (b) da questão quer saber quanto vale a taxa de transferência de calor que a parede conduz, dividida pela área da parede. Ou seja,, a questão quer saber agora quanto vale . Podemos fazer esse cálculo tanto pela lei de Fourier quanto pela lei de resfriamento de Newton. Escolhemos então, sem nenhum motivo especial, a segunda opção:
Aeeee! Essa foi a letra (b) da questão! Bem mais rápida, né?