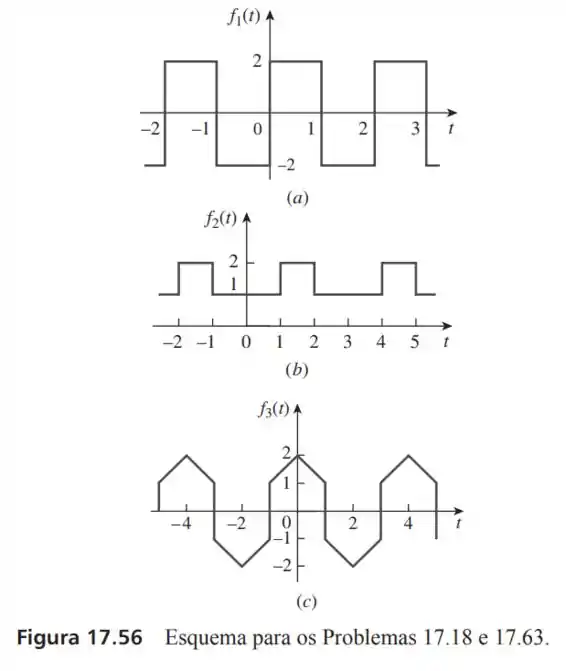
18- Determine a frequência fundamental e especifique o tipo de simetria presente nas funções da Figura .
Passo 1
Além das simetrias par ou ímpar (que são simetrias em relação ao eixo vertical ) temos a simetria em relação ao eixo que é a simetria de meia onda. Onde a função positiva tem que ser o inverso da função negativa na metade do período.
Imaginando que o período de uma onda é de , para ela ser de meia onda ela tem que ter o seguinte comportamento:
Passo 2
Na letra temos uma onda com período igual a e portanto
E um comportamento igual a:
Como a função assume o mesmo módulo na parte de cima e na parte de baixo, então a onda tem simetria de meia onda . E simetria ímpar pois e .
Passo 3
Já tem um príodo de e portanto um e seu comportamento é igual a:
Essa simetria não acontece horizontalmente, então o eixo não corta a onda em duas metades. E e portanto a simetria é par.
Passo 4
O período dessa onda é de até , portanto de , o que nos leva a uma onda de .
E como a reta que cresce de até é simétrica a reta que decresce de até e os valores de máximo dessa onda são de até então a onda é simetrica pelo eixo x, tendo uma simetria de meia onda. Além de que , portanto temos uma simetria par.