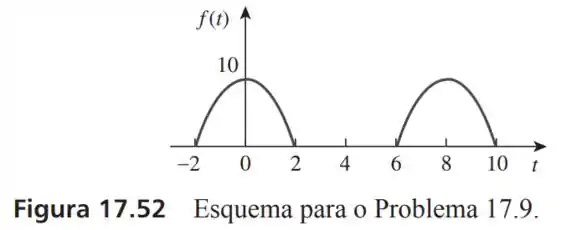
9- Determine os coeficientes de Fourier e dos três primeiros termos harmônicos da onda cosseno retificada da Figura .
Passo 1
Essa função tem um período igual a:
Então será:
Dessa forma a equação de é:
E vamos dizer que o período dessa onda vai de até e amplitude desse cosseno é de .
Passo 2
Então será:
Ou só vezes a integral indo de até .
Passo 3
Agora será:
Dessa forma teremos para :
Essas duas últimas integrais foi necessário utilizar ferramenta computacional.
Passo 4
A função é uma função par , então por tabela sabemos que .
Logo