Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 19

19- Obtenha a série de Fourier para a forma de onda periódica da Figura 17.57 .

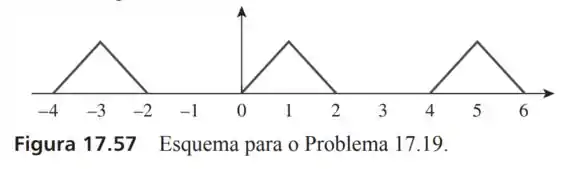
Passo 1

O período dessa onda vai de 0 até 4 , então:

T = 4 ; ω = π 2

E o comportamente dessa função vale:

f t = t ; 0 < t < 1

Supondo que a onda vai até y t = 1 por que né... o desenho não mostra...

f t = 2 - t ; 1 < t < 2

Passo 2

O valor de a 0 será:

a o = 1 4 ∫ 0 1 t   d t + ∫ 1 2 2 - t d t

a 0 = 1 4 t 2 2 0 1 + 2 t - t 2 2 1 2

a 0 = 1 4 1 2 + 4 - 2 - 2 + 1 2 = 1 4 = 0.25  

Passo 3

O valor de a n será:

a n = 2 4 ∫ 0 1 t cos ⁡ n π t 2 d t + ∫ 1 2 2 - t cos ⁡ n π t 2 d t

Onde:

∫ t c o s n π t 2 d t = 4 π 2 n 2 π n 2 t   s i n π n t 2 + cos ⁡ π n t 2 d t

a n = 1 2 ( 4 π 2 n 2 π n 2 t   s i n π n t 2 + cos ⁡ π n t 2 0 1 - 4 π 2 n 2 π n 2 t   s i n π n t 2 + cos ⁡ π n t 2 1 2 + …

4 π n sin ⁡ π n t 2 1 2 )

Como cos ⁡ π n = - 1 n

a n = 2 π 2 n 2 π n 2 sin ⁡ π n 2 + cos ⁡ π n 2 - 1 - 2 π 2 n 2 - 1 n - π n 2 sin ⁡ π n 2 - cos ⁡ π n 2

- 2 π n sin ⁡ π n 2

a n = - 2 π n sin ⁡ π n 2 + 4 π 2 n 2 π n 2 sin ⁡ π n 2 + cos ⁡ π n 2 - 2 π 2 n 2 - 2 π 2 n 2 - 1 n

Passo 4

E o valor de b n será:

b n = 1 2 ∫ 0 1 t sin ⁡ n π t 2 d t + ∫ 1 2 2 - t sin ⁡ n π t 2 d t

Onde:

∫ t sin ⁡ n π t 2 d t = 4 π 2 n 2 - π 2 n t cos ⁡ π n t 2 + sin ⁡ π n t 2

Então:

b n = 1 2 ( 4 π 2 n 2 - π 2 n t cos ⁡ π n t 2 + sin ⁡ π n t 2 0 1 + 4 π 2 n 2 - π 2 n t cos ⁡ π n t 2 + sin ⁡ π n t 2 1 2

- 4 π n cos ⁡ n π t 2 1 2 )  

Uma vez que cos ⁡ n π = sin ⁡ π n 2 = - 1 n

b n = 2 π n - - 1 n + cos ⁡ π n 2 - 2 π 2 n 2 - π n - 1 n + π n 2 cos ⁡ π n 2 - sin ⁡ π n 2

+ 2 π 2 n 2 sin ⁡ π n 2 - π n 2 cos ⁡ π n 2

b n = 2 π n cos ⁡ π n 2 - 4 π 2 n 2 π n 2 cos ⁡ π n 2 + sin ⁡ π n 2

Colocando esses valores de a n e b n temos:

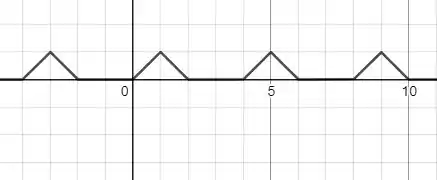
Então a equação da série será:

f x = 0.25 + ∑ n = 1 ∞ - 2 π n sin ⁡ π n 2 + 4 π 2 n 2 π n 2 sin ⁡ π n 2 + cos ⁡ π n 2 - 2 π 2 n 2 - 2 π 2 n 2 - 1 n cos ⁡ n π t 2 + = 2 π n cos ⁡ π n 2 - 4 π 2 n 2 π n 2 cos ⁡ π n 2 + sin ⁡ π n 2 sin ⁡ n π t 2

Não posso falar um palavrão aqui, mas nossa que integrais chatas hahahahaha namoral...

Resposta

f x = 0.25 + ∑ n = 1 ∞ - 2 π n sin ⁡ π n 2 + 4 π 2 n 2 π n 2 sin ⁡ π n 2 + cos ⁡ π n 2 - 2 π 2 n 2 - 2 π 2 n 2 - 1 n cos ⁡ n π t 2 + = 2 π n cos ⁡ π n 2 - 4 π 2 n 2 π n 2 cos ⁡ π n 2 + sin ⁡ π n 2 sin ⁡ n π t 2

Ver Outros Exercícios desse livro