Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 22
22. Determine o menor valor da onda senoidal deslocada abaixo:
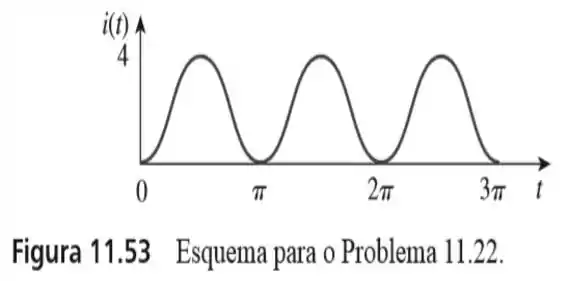
Passo 1
Primeiro, temos que encontrar a expressão de . Analisando a onda, vemos que seu período é . Logo:
Como:
Temos então, que:
Além disso, o seu valor de um pico ao outro é . Portanto, sua amplitude será:
Como ele me disse que é uma onda que representa uma corrente, já sabemos que parte da expressão terá o termo abaixo:
Pois correntes são dadas em função de cossenos!
Passo 2
Agora, vamos analisar o deslocamento. Para isso, vamos escolher um ponto do gráfico. Por exemplo, a origem . Substituindo na expressão que temos até agora:
No gráfico, quando a corrente vale zero. Logo, para nossa expressão estar de acordo com a onda do gráfico, precisamos que o seu valor na origem seja zero. Temos duas formas de faze isso:
Para verificarmos qual é a que corresponde ao gráfico, vamos escolher um novo ponto. Por exemplo, quanto .
Substituindo em :
Esse resultado bate bem com o gráfico! Logo a expressão que descreve o gráfico é:
Passo 3
Agora, vamos calcular o valor :
Lembrando que a integral ao longo do período de uma função senoidal é zero:
e da relação:
Temos que: