Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 93

Considere o circuito deslocador de fase mostrado na figura e determine H = V 0 / V s

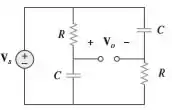
Passo 1

Para começar esse problema, vamos nomear a tensão no ramo 1 (ramo do meio) de V 1 e a do ramo lateral de V 2 :

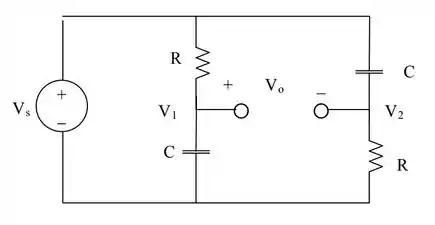
Bem, de a diferença de tensão V 0 então é dada por:

V 0 = V 1 - V 2

Devemos então descobrir quem é V 1 e V 2 em termos de V s para então descobrir H depois! Bora?

Passo 2

A tensão V 1 pode ser encontrada pela Lei de Ohm:

V 1 = I 1 ⋅ X c   →

Onde I 1 é a corrente no ramo 1 , enquanto que X c é a reatância capacitiva. Onde ela vale sempre:

X c = 1 j ω C

A corrente I 1 , entretanto, pode ser obtida observando que a tensão V s está sobre o todos os elementos do ramo 1 . A impedância total desse ramo, podemos chamar de Z 1 , e também pela Lei de Ohm:

I 1 = V s Z 1

Onde...

Z 1 = R + X c   →

Z 1 = R + 1 j ω C  

Logo, substituindo e simplificando...

V 1 = I 1 ⋅ X c   →

V 1 = V s Z 1 ⋅ X c   →

V 1 = 1 j ω C R + 1 j ω C   V s

Passo 3

Podemos fazer a mesma análise para encontrar V 2 , que dessa vez será...

V 2 = I 2 ⋅ R

Onde o I 2 , pelo divisor de correntes...

I 2 = V s Z 2

O Z 2 é a impedância total no ramo 2 e ela é exatamente a mesma coisa que Z 1 , já que ambas são formadas por um Resistor R e um Capacitor C , só que com ordens trocadas. Então teremos:

I 2 = V s R + 1 j ω C

V 2 = I 2 ⋅ R = R R + 1 j ω C ⋅ V s

Passo 4

Como vimos, V 0 é dado por:

V 0 = V 1 - V 2

Substituindo e simplificando...

V 0 = 1 j ω C R + 1 j ω C ⋅ V s - R R + 1 j ω C   V s   →

V 0 = 1 j ω C - R 1 j ω C + R ⋅ V s   →

Passando esse V s dividindo, ganharemos o H (lembre-se que para simplificar o problema, podemos substituir esse j ω por s ):

H = V 0 V s = 1 s C - R 1 s C + R

Ou ainda, tirando o MMC das frações...

H = 1 - s R C 1 + s R C

Resposta

H = 1 - s R C 1 + s R C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O circuito mostrado na figura tem impedância Z ( s ) = 1000 ( s + 1 ) ( s + 1 + j 50 ) ( s + 1 - j 50 ) ,s = j ω Determine: Os valores de R ,L ,CeG Os valores dos elementos que farão que a frequência
Um circuito R L C em série possui R = 10 Ω ,ω o = 40r a d / seB = 5r a d / s . Determine LeC quando o circuito sofre uma aplicação de escala: Na amplitude por um fator 600 . Na frequência por um fator
Observe o circuito da figura. Determine Z e n t ( s ) Aplique fatores de escala K m = 10eK f = 100 aos elementos. Determine Z e n t ( s )eω o .
Redesenhe o circuito da figura, de modo que todos os elementos resistivos sofram um fator de escala 1000 e todos os elementos sensíveis à frequência sofram um fator de escala 1 0 4 .
Use fatores de escala de amplitude e de frequência no circuito da figura para obter um circuito equivalente no qual o indutor e o capacitor possuem, respectivamente, valores de 1 He1 F .