Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 33

33- Determine o valor R M S para a forma de onda na Figura 11.64

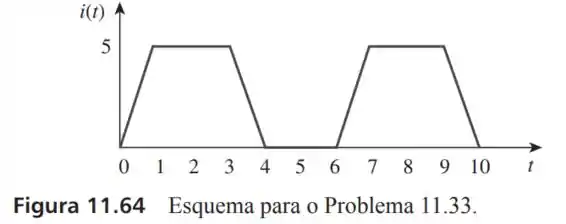
Passo 1

Podemos dividir a onda trapezoidal da figura em 4 regiões. Acompanha o raciocínio

De 0 até 1 segundo- Uma reta crescente com comportamento igual a f t = 5 t pois em 1   s ele vale 5

De 1 segundo até 3 segundos- Uma reta constante de valor igual a f t = 5

De 3 segundos até 4 segundos- Uma reta decrescente com comportamento igual a f t = - 5 t , pois em uma segundo ela decresce 5, só que para não tirar a equação da reta cruzando as retas i e t nós devemos escrever que ela varia de 0 até 1.

De 4 segundos até 6 segundos- Uma reta nula, f t = 0

Passo 2

Dessa forma a integral do R M S será:

I R M S = 1 6 ∫ 0 1 5 t 2 d t + ∫ 1 3 5 2 d t + ∫ 0 1 - 5 t 2 + ∫ 4 6 0   d t

Fazendo isso:

I R M S = 1 6 25 t 3 3 0 1 + 25 t 1 3 + 25 t 3 3 0 1

I R M S = 1 6 25 3 + 50 + 25 3 = 3.333   A

Resposta

I R M S = 3.333   A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

27. Calcule o valor R M S da forma de onda de corrente da figura 11.58
13. A impedância de T h é v e n i n é de uma fonte é Z T h = 120 + j 60Ω , enquanto a tensão de T h é v e n i n é de pico é V T h = 165 + j 0 V . Determine a potência máxima disponível da fonte.
22. Determine o menor valor R M S da onda senoidal deslocada abaixo:
8. No circuito da figura 11.40 determine a potência média absorvida pelo resistor de 40Ω .
29- Calcule o valor eficaz da forma de onda da corrente mostrada na Figura 11.60 e a potência média liberada para um resistor de 12Ω , quando a corrente percorre o resistor.