Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 25

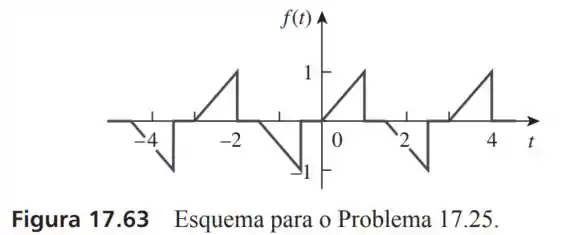
25- Determine a representação da série de Fourier da função na Figura 17.63

Passo 1

O período dessa onda vai de 0 até 3 portanto:

T = 3 → ω = 2 π 3

E essa onda é uma onda com simetria de meia onda pois a parte a cima do eixo t é inversa da parte de baixo dessa reta, portanto:

a 0 = 0

Além de a n = b n = 0 para n ímpar.

Então teremos o seguinte comportamento de onda:

f t = t ; 0 < t < 1

f t = 0 ; 1 < t < 1.5

Onde temos que fazer a integral de 2 vezes esse intervalo para encontrar a n e b n

Passo 2

O valor de a n será:

a n = 4 3 ∫ 0 1 t cos ⁡ 2 π n 3 t   d t

A integral de t cos ⁡ 2 π n t 3 será:

∫ t cos ⁡ 2 π n t 3 d t = 9 4 π 2 n 2 2 π 3 n t s i n 2 π n t 3 + cos ⁡ 2 π n t 3

Então:

a n = 3 π 2 n 2 2 π 3 n t s i n 2 π n t 3 + cos ⁡ 2 π n t 3 0 1

Substituindo os termos temos:

a n = 3 π 2 n 2 2 π n 3 sin ⁡ 2 π n 3 + cos ⁡ 2 π n 3 - 1

Passo 3

Agora para b n :

b n = 4 3 ∫ 0 1 t sin ⁡ 2 π n 3 t d t

Onde a integral de t sin ⁡ 2 π n t 3 é:

∫ t s i n 2 π n t 3 d t = 9 4 π 2 n 2 - 2 π n 3 cos ⁡ 2 π n 3 t + sin ⁡ 2 π n 3 t

Dessa forma:

b n = 3 π 2 n 2 - 2 π n t 3 cos ⁡ 2 π n 3 t + sin ⁡ 2 π n 3 t 0 1

b n = 3 π 2 n 2 - 2 π n 3 cos ⁡ 2 π n 3 + sin ⁡ 2 π n 3

Por conta disso a equação de Fourier será:

f t = ∑ k = 1 ∞ 3 π 2 n 2 2 π n 3 sin ⁡ 2 π n 3 + cos ⁡ 2 π n 3 - 1 cos ⁡ 2 π n t 3 +

3 π 2 n 2 - 2 π n 3 cos ⁡ 2 π n 3 + sin ⁡ 2 π n 3 sin ⁡ 2 π n t 3

Com k = 2 n - 1

Colocando esses valores em um gráfico nós teremos:

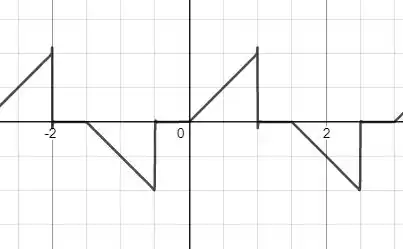
Valores certinhos

Resposta

f t = ∑ k = 1 ∞ 3 π 2 n 2 2 π n 3 sin ⁡ 2 π n 3 + cos ⁡ 2 π n 3 - 1 cos ⁡ 2 π n t 3 +

3 π 2 n 2 - 2 π n 3 cos ⁡ 2 π n 3 + sin ⁡ 2 π n 3 sin ⁡ 2 π n t 3

Com k = 2 n - 1

Ver Outros Exercícios desse livro