A tensão senoidal retificada de onda completa, indicada na figura a, é aplicada ao filtro passa baixas da figura b. Obtenha a tensão de saída do filtro.
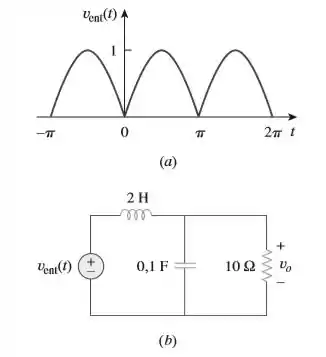
Passo 1
Essa questão vai ser lonnnnga! Já vou avisando haha
Primeiro, devemos perceber quo período da função é ...
Onde de a ela é uma crista de um seno:
Perceba que seno de é , o que corresponde certinho com a nossa curva !
Primeiro vamos ter que descrever esse sinal periódico em termos de cossenos (série de Fourier) e para isso, temos que encontrar os seus coeficientes encontrados assim:
Passo 2
Primeiro calculemos o ...
Agora vamos encontrar :
Calculando essa integral por partes vamos obter...
Agora vem a substituição. Ora de se tomar cuidado aonde você vai substituir...
Lembrando que é para ímpar e para os pares, a gente ganha o seguinte:
Podemos encontrar por cálculos semelhantes...
Mas como se trata de uma onda periódica de simetria par (ela tem simetria no eixo ), então...
Passo 3
Beleza! Com esses coeficientes calculados, podemos determinar qual é o nosso sinal apenas por cossenos lembrando-se da definição de Fourier para apenas cossenos:
Como foi separado em e ...
Vamos separar o somatório também:
Não se esqueça do ...
Passo 4
Bem, pelo fato da equação de cima ter uma constante a parte, isso significa que o nosso circuito vai possuir uma componente :
A parte oscilatória a componente :
Vamos primeiro trabalhar com a componente .
Passo 5
Ora, sabemos que para um circuito (), o capacitor é um circuito aberto e o indutor um curto:
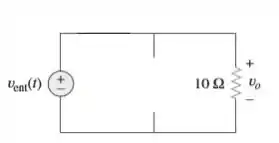
Passo 6
Agora vamos resolver para as componentes . Nesse caso é considerado o circuito todo...
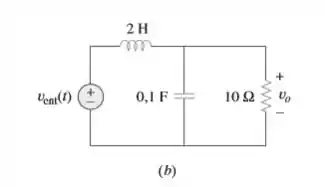
E como a gente está lidando com domínio da frequência é conveniente mudarmos para o munda das impedâncias...
Onde esse nada mais é do que as frequências discretas (o cara que multiplica no cosseno):
Então...
Enfim, pela divisão de corrente...
Sendo ...
Então...
Passo 7
Parece que acabou, pois encontramos o , na verdade o que encontramos foram dois : um :
E um :
No domínio da frequência eles não se misturam, mas se passarmos para o domínio do tempo ...
Onde...
Elas se misturam. E essa é a resposta final já que nos dá uma única resposta para o pedido.
Resposta
Onde...