Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 52
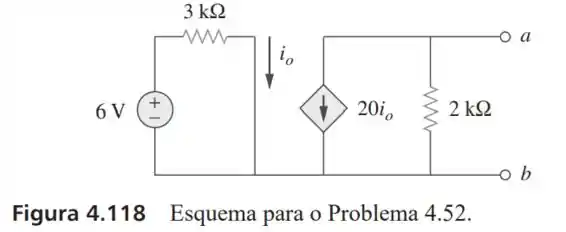
52- Para o modelo de transistor da Figura , obtenha o equivalente de Thévenin nos terminais .
Passo 1
Para encontrar precisamos ver que o terminal onde está conectado o terminal do resistor vale dessa forma:
Dessa forma podemos analisar a malha de circuito a direita para encontrarmos a tensão de Thévenin.
Como a corrente que passa pelo resitor de vale então será:
Só que como a tensão em vale , logo para a tensão em será negativa, para que a corrente flua de para , então:
Passo 2
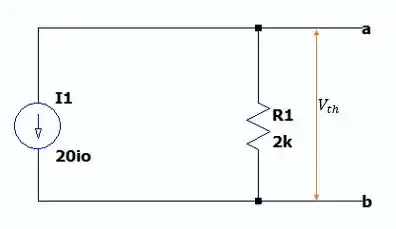
Agora basta encontrarmos a resistência de Thévenin para que possamos fechar a questão, porém note que se fecharmos o contato entre e nós não teremos corrente nenhuma passando pelo resistor de nos dando uma corrente de Norton igual a da fonte dependente que vale:
E se calcularmos a resistência de Thévenin vamos obter:
Que é igual a resistência conectada entre os terminais, sem depender do circuito que vem antes. E acredite por ser simples assim esse modelo de transistor em bastante usado em muitos programas computacionais e é bastante eficiente, mais tarde quem for fazer Eletrônica vai ver esse bastante esse modelo.