Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 69
69. Um voltímetro é usado para medir no circuito da Figura . O modelo do voltímetro consiste em um voltímetro ideal em paralelo com um resistor de . Digamos que , e . Calcule com e sem o voltímetro quando:
a)
b)
c)
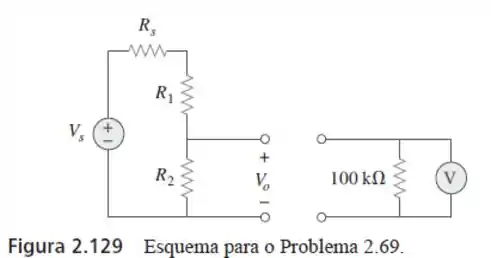
Passo 1
Bom! Vamos tentar descobrir equações gerais para os casos em que existe ou não, a presença do voltímetro.
Olha só! No caso em que há a presença do voltímetro, podemos ver que as resistências de e estão em paralelo. Sendo assim, por divisão de tensão obtemos facilmente que nosso é dado pela seguinte relação abaixo:
Já para o caso em que não há a presença do voltímetro, também por divisão de tensão, obtemos que é dado por:
E uma vez que o enunciados já nos fornece os valores de , e ; basta substituir os valores de fornecidos, que obtemos a resposta para cada letra.
Passo 2
a) Bora fazer o cálculo pra essa letra, onde :
Primeiro, o caso com voltímetro:
Depois, para o caso sem voltímetro:
Passo 3
b) Bora fazer o cálculo pra essa letra agora, onde :
Primeiro, o caso com voltímetro:
Depois, para o caso sem voltímetro:
Passo 4
c) E por último, o cálculo pra :
Primeiro, o caso com voltímetro:
Depois, para o caso sem voltímetro:
Missão cumprida!
Resposta
a)
b)
c)