Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 79

79- Determine a leitura do wattímetro no circuito da Figura 11.94 .

Passo 1

A fonte de 10 cos ⁡ 100 t   é uma fonte que não está em R M S e ela excita todo o circuito com um ω = 100 . Então as reatâncias no capacitor e no indutor será:

X C = - j ω C = - j 100 × 500 × 10 - 6 = - 20 j

X L = j ω L = j 100 × 10 × 10 - 3 = j

Então sabendo que essa fonte representa um fasor de 10 ∠ 0 temos oseguinte circuito.

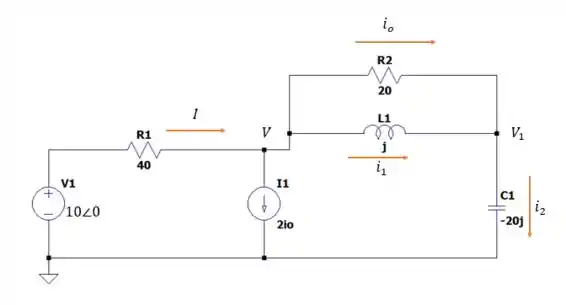
E precisaremos da tensão V e da corrente I para fazer:

S = 1 2 V I *

Passo 2

Aanalisando todas as correntes que entram e saem no nó de tensão igual a V nós teremos:

I = 2 i o + i o + i 1

Isso é:

10 - V 40 = 3 V - V 1 20 + V - V 1 j

10 - V 40 = 3 V j - 3 V 1 j + 20 V - 20 V 1 20 j

1 4 = V 40 + V 20 + 3 j - V 1 ( 20 + 3 j ) 20 j

1 4 = 20 j V 800 j + 40 V 20 + 3 j - 40 V 1 ( 20 + 3 j ) 800 j

200 j = V 800 + 140 j - V 1 ( 800 + 120 j )

Agora as correntes que entram no nó de tensão igual a V 2 temos:

i o + i 1 = i 2

V - V 1 20 + V - V 1 j = V 1 - 20 j

V 20 + j - V 1 ( 20 + j ) 20 j = V 1 - 20 j

V ( 20 + j ) - V 1 20 + j = - V 1

V 20 + j = V 1 ( 19 + j )

V 1 = V 20.02 ∠ 2.862 ° 19.026 ∠ 3.013 ° = V 1.0522 ∠ - 0.151 °

Substituindo esse resultado na primeira equação nós temos:

200 j = V 800 + 140 j - V 1.0522 ∠ - 0.151 ( 800 + 120 j )

200 j = V 812.16 ∠ 9.926 - V ( 851.18 ∠ 8.38 )

V = 200 ∠ 90 812.16 ∠ 9.926 - 851.18 ∠ 8.38 = 200 ∠ 90 - 42.09 + j 15.95 = 200 ∠ 90 45.01 ∠ 159.246

V = 4.44 ∠ - 69.246 = 1.573 - j 4.15   Ω

Passo 3

Agora calculando I :

I = 10 - 1.573 + j 4.15 40 = 0.211 + j 0.1038 = 0.235 ∠ 26.2

Então a potência complexa será:

S = 1 2 4.44 ∠ - 69.246 0.235 ∠ - 26.2 = 0.5216 ∠ - 95.446

Então P será:

P = 0.5216 cos ⁡ - 95.446 = - 50   m W

Ou:

P = 50   m W

Resposta

P = 50   m W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

29- Calcule o valor eficaz da forma de onda da corrente mostrada na Figura 11.60 e a potência média liberada para um resistor de 12Ω , quando a corrente percorre o resistor.
31- Determine o valor R M S do sinal indicado na Figura 11.62 .
30- Calcule o valor R M S da forma de onda representado na Figura 11.61 .
Se a impedância da carga for 20 - j 20 , o fator de potência será: ∠ - 45 ° 0 1 0,7071 Nenhuma das alternativas anteriores