Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 35

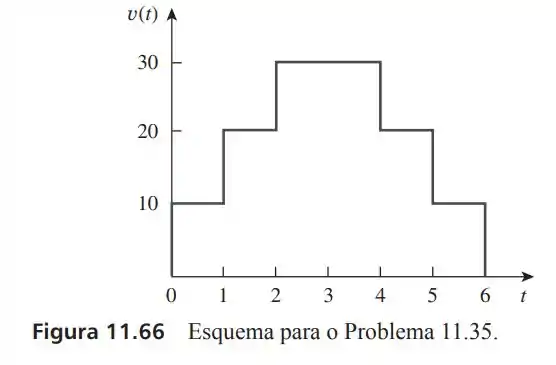
35- Um ciclo de uma forma de onda periódica é representado na Figura 11.66 . Determine o valor eficaz da tensão. Note que o ciclo se inicia em t = 0 e termina em t = 6   s

Passo 1

Não é por que a figura é simétrica que o período dele esteja bem na metade do tempo. A onda ela tem que crescer, descer e voltar a posição original (onde o sinal vai crescer de novo, se descer é por que o período dele está em outro lugar). Dessa forma podemos dividir a onda em cinco regiões verticais.

0   a   1 s → v t = 10

1   a   2 s → v t = 2 0

2   a   4 s → v t = 3 0

4   a   5 s → v t = 2 0

5   a   6 s → v t = 10

Passo 2

Deixando nossa integral de R M S da seguinte forma:

v R M S = 1 6 ∫ 0 1 10 2 d t + ∫ 1 2 20 2 + ∫ 2 4 30 2   d t + ∫ 4 5 20 2 + ∫ 5 6 10 2   d t

Logo:

v R M S = 1 6 [ 100 + 400 + 2 × 900 + 400 + 100 ] = 21.602   V

Resposta

v R M S = 21.602   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

34- Determine o valor eficaz de f ( t ) definida na Figura 11.65
32- Obtenha o valor R M S da forma de onda corrente mostrada na Figura 11.63 .
33- Determine o valor R M S para a forma de onda na Figura 11.64
37- Elabore um problema para ajudar outros estudantes a entender melhor como determinar o valor R M S da soma de correntes múltiplas
36- Calcule o valor R M S para cada uma das seguintes funções: ( a ) i t = 10A ( b ) v t = 4 + 3 cos ⁡ 5 tV ci t = 8 - 6s e n2 tA ( d ) v t = 5s e nt + 4 cos ⁡ tV