Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas Abrangentes - Ex. 83
83. Dois dispositivos são especificado conforme mostra a Figura 2.142. Determine os valores dos resistores e necessários para alimentar os dispositivos usando uma bateria de .
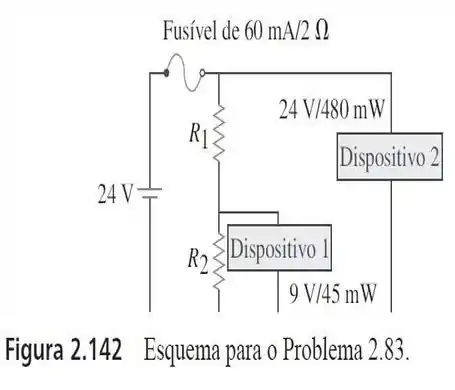
Passo 1
Bom! A A tensão no fusível deve ser insignificante quando comparada a (isso pode ser verificado posteriormente quando verificamos se a classificação do fusível foi excedida no circuito final). Podemos calcular a corrente através dos dispositivos, simplismente dividindo a potência pela tensão correspondente:
Passo 2
Agora, vamos fazer um esboço de como as corrente estão distribuídas ao longo do nosso circuito:
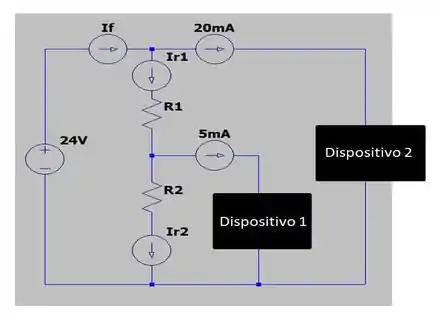
E uma vez que representa a resistência do primeiro dispositivo, podemos determinar seu valor apenas conhecendo a tensão e a corrente através dele, do seguinte jeito:
Passo 3
Agora presta atenção numa coisa. Esse é um problema interessante, pois ele possui basicamente duas incógnitas, e , mas apenas uma condição que precisa ser atendida é que a tensão em deve ser igual a . Como o circuito é alimentado por uma bateria, podemos escolher o valor de que consome a menor corrente, . Assim, podemos calcular o valor de que fornece 9 volts usando divisão de tensão:
Esse valor de significa que temos apenas um total de saindo da bateria pelo fusível, o que significa que ela não abre e produz uma queda de tensão através dele de . Isso é realmente insignificante quando comparado com a fonte de .