Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas Abrangentes - Ex. 82

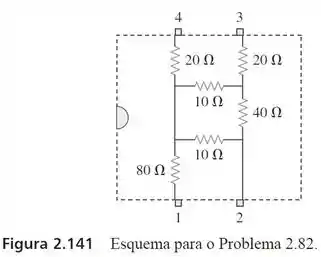
82. O diagrama de pinos de um conjunto de resistências está representado na Figura 2.141. Determine a resistência equivalente entre os seguintes pinos:

a) 1   e 2

b) 1   e 3

c) 1   e 4

Passo 1

a) Bom! Nessa primeira letra, como o que queremos é a resistência equivalente entre 1 e 2 , iremos desprezar qualquer resistência que faça interação com 3 e 4 .

Ou seja, iremos aproveitar apenas a seguinte parte do circuito:

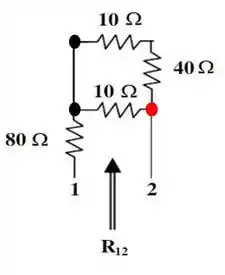
Onde a resistência equivalente R 12 é dada por:

R 12 = 80   Ω + ( 10   Ω ) | | 10   Ω + 40   Ω

R 12 = 80   Ω + ( 10   Ω ) | | ( 50   Ω )

R 12 = 80   Ω + 10   Ω ⋅ 50   Ω 10   Ω + 50   Ω

R 12 = 80   Ω + 10   Ω ⋅ 50   Ω 10   Ω + 50   Ω

R 12 = 80   Ω + 50 6 Ω

R 12 = 88,33   Ω

Passo 2

b) Já nessa segunda letra, como o que queremos é a resistência equivalente entre 1 e 3 , iremos desprezar qualquer resistência que faça interação direta com 2 e 4 .

Ou seja, iremos aproveitar apenas a seguinte parte do circuito:

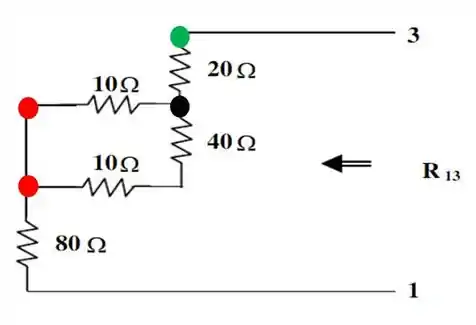
Onde a resistência equivalente R 13 é dada por:

R 13 = 80   Ω + ( 10   Ω ) | | 10   Ω + 40   Ω + 80   Ω

R 13 = 100   Ω + ( 10   Ω ) | | ( 50   Ω )

R 13 = 100   Ω + 10   Ω ⋅ 50   Ω 10   Ω + 50   Ω

R 13 = 100   Ω + 10   Ω ⋅ 50   Ω 10   Ω + 50   Ω

R 13 = 100   Ω + 50 6 Ω

R 13 = 108,33   Ω

Passo 3

c) Nessa última letra, como o que queremos é a resistência equivalente entre 1 e 4 , iremos desprezar qualquer resistência que faça interação direta com 1 e 3 .

Ou seja, iremos aproveitar apenas a seguinte parte do circuito:

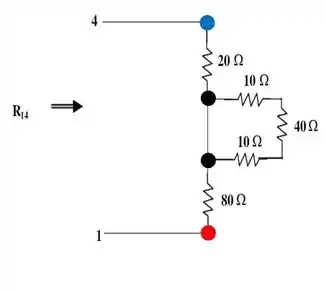
Onde a resistência equivalente R 14 é dada por:

R 14 = 80   Ω + ( 0   Ω ) | | 10   Ω + 10   Ω + 40   Ω + 20   Ω

R 14 = 100   Ω + 0   Ω ⋅ 60   Ω 0   Ω + 60   Ω

R 14 = 100   Ω

Resposta

a) R 12 = 88,33   Ω  

b) R 13 = 108,33   Ω  

c) R 14 = 100   Ω  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o circuito da figura 2.90 , i 0 = 3 A . Calcule i x e a potência total dissipada pelo circuito.
Calcule I 0 no circuito da figura 2.91 .
Determine a R e q para o circuito da figura 2.94 .
Usando associações de resistências em série/paralelo, determine a resistência equivalente vista pela fonte no circuito da figura 2.98 e a potência total dissipada pela rede de resistores.