Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas Abrangentes - Ex. 81

81. Em determinada aplicação, o circuito da Figura 2.140 tem de ser projetado de forma a atender a dois critérios a seguir:

a) V 0 / V s = 0,05

b) R e q = 40   k Ω

Se o resistor de carga de 5   k Ω     for fixo, determine R 1 e R 2 para atender aos critérios.

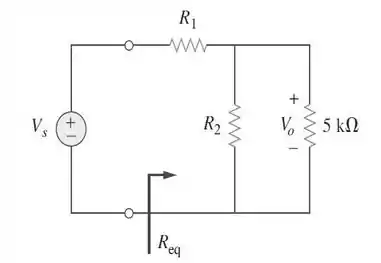
Passo 1

Bom! Vamos dar uma olha nesse circuito novamente:

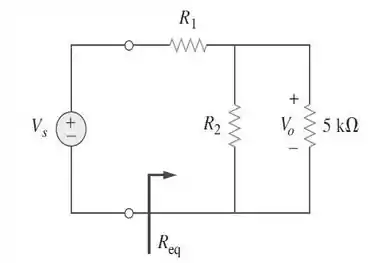
Analisando ele novamente, podemos ver que a resistência equivalente é dada por:

R e q = R 1 + ( R 2 | | 5 )   k Ω

E por divisão de tensão, temos que V 0 é dada por:

V 0 = ( R 2 | | 5 )     k Ω R 1 + ( R 2 | | 5 )   k Ω ⋅ V s

V 0 V s = ( R 2 | | 5 )     k Ω R 1 + ( R 2 | | 5 )   k Ω

Como sabemos que V 0 / V s deve ser igual a 0,05 e que   R e q deve valer 40   k Ω .... Então, obtemos que:

V 0 V s = ( R 2 | | 5 )     k Ω R 1 + ( R 2 | | 5 )   k Ω

V 0 V s = ( R 2 | | 5 )     k Ω R e q   k Ω

0,05 = ( R 2 | | 5 )     k Ω 40   k Ω

0,05 = R 2 ⋅ 5 R 2 + 5   40

R 2 ⋅ 5 R 2 + 5 = 2

5 R 2 = 2 R 2 + 10

3 R 2 = 10

R 2 = 10 3   k Ω

Passo 2

Uma vez que R 2 = 10 / 3   k Ω ...

Usando a equação abaixo, podemos obter o valor de R 1 :

R e q = R 1 + ( R 2 | | 5 )   k Ω

40   k Ω = R 1 + 10 3 ⋅ 5 10 3 + 5   k Ω

40   k Ω = R 1 + 2   k Ω

R 1 = 40   k Ω - 2   k Ω

R 1 = 38   k Ω

Resposta

R 1 = 38   k Ω

R 2 = 10 3   k Ω

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

a) Determine a resistência vista pela fonteideal de tensão no circuito da Figura P3.60.b) Se vab for igual a 400 V, qual será a potência dissipada no resistor de 31 V?
Determine io e a potência dissipada no resistor de 140 V do circuito da Figura P3.62.
Redes de resistores são, às vezes, utilizadas como circuitos de controle de volume. Nessa aplicação, elas são denominadas atenuadores resistivos ou atenuadores fixos.Um atenuador fixo típico é mostrad
Deduza as equações 3.44–3.49 a partir das equações 3.41–3.43. As duas sugestões a seguir vão ajudá-lo a tomar a direção correta:1) Para determinar R1 em função de R a, R b e R c, em primeiro lugar, su
Para o circuito mostrado na Figura P3.63, determine (a) i 1, (b) v, (c) i 2 e (d) a potência fornecida pela fonte de tensão.