Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 92

92- Considere a ponte da Figura 4.148 . A ponte se encontra equilibrada? Se o resistor de 10   k Ω for substituído por um resistor de 18   k Ω , que resistor conectado entre os terminais absorve a potência máxima? Qual é essa potência?

Passo 1

Para a ponte estar equilibrada o produto entre os resistores opostos deverão ser iguais, ou seja:

3 k × 10 k = 5 k × 6 k

O que nos:

30   M = 30   M

Onde k = 10 3 e M = 10 6 .

Logo sim a ponte está equilibrada.

Entenda, a ponte estar equilibrado como:

V t h = 0 ; I N = 0  

Isso é, não há passagem de corrente pelos terminais a - b caso elas estejam fechadas.

Passo 2

Agora substituindo o resistor de 10   k Ω por um de 18   k Ω teremos o seguinte circuito.

Retirando a fonte e o aterramento para descobrirmos a resistência de Thévenin nós teremos:

Aí para fazer essa questão nós devemos lembrar da transformação de Delta para estrela ( que é bem difícil de alguem lembrar depois de uns três dias).

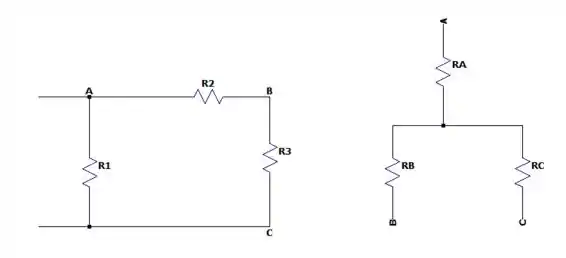
O primeiro é o caso Delta e o segundo o estrela, para transformar um em outro temos que fazer.

R A = R 1 R 2 R 1 + R 2 + R 3

R B = R 3 R 2 R 1 + R 2 + R 3

R C = R 1 R 3 R 1 + R 2 + R 3

Então com o exemplo que temos vamos tratar a malha de 3 k , 6 k e 2 k com nossa malha Δ . Isso nos daria uma transformação igual a:

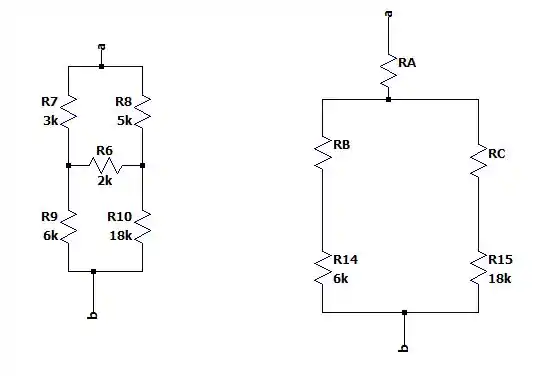
Isso seria:

R A = 3 k 5 k 3 k + 5 k + 2 k = 1 . 5   k Ω

R B = 3 k 2 k 3 k + 5 k + 2 k = 0 . 6   k Ω

R C = 2 k 5 k 3 k + 5 k + 2 k = 1   k Ω

Então a resistência equivalente da malha toda será de:

R t h = 1 . 5 k Ω + 1 1 ( 6 k + 0 . 6 k ) + 1 ( 1 k + 18 k ) = 6.398   k Ω

Passo 3

Agora vamos encontrar V t h encontrando as tensões de v a e de v b no circuito abaixo:

Fazendo a somatória das correntes temos:

i t = i 1 + i 2

Onde:

V o = 3 k + 5 k i 1 = 18 k + 6 k i 2

V o = 8 k i 1 = 24 k i 2

Além de que:

220 - V o = 2 k i t

V o = 220 - 2 k i t

Isolando todas as correntes temos:

i t = 220 - V o 2 k ; i 1 = V o 8 k ;     i 2 = V o 24 k

Substituindo tudo na equação de soma das correntes teremos:

220 - V o 2 k = V o 8 k + V o 24 k

O que nos dá um valor de V o igual a:

0.11 - V o 2 k = 4 24 k V o → V o = 165   V

Isso nos dá correntes i 1 e i 2 iguais a:

i 1 = 20.625   m A ; i 2 = 6.875   m A

Dessa forma finalmente poderemos calcular as tensões v a e v b :

V o - v a = 3 k i 1 → v a = 165 - 3 k × 20.625 m = 103.125   V

V o - v b = 6 k i 2 → v b = 165 - 6 × 6.875 = 123.75   V

Então a tensão de Thévenin será:

V t h = v a - v b = 103.125 - 123.75 = - 20.625   V

Passo 4

Com a tensão e a resitência de Thévenin calculadas vamos calcular a maior potência possível:

p m a x = V t h 2 4 R t h = 20.625 2 4 × 6.398 × 10 3 = 16.62   m W

Resposta

A ponte está equilibrada.

Para R = 18   k Ω ao invés de 10   k Ω

R t h = 6.398   k Ω

p m a x = 16.62   m W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o equivalente de Thevenin de tudo, exceto o resistor de 4Ω no Prob. 5.16, e use o resultado para encontrar a potência entregue ao resistor de 4Ω .
Substitua a rede à esquerda dos terminais a-b pelo seu equivalente de Thevenin e use o resultado para calcular i .
Calcule v pela substituição de tudo, menos o resistor de 4 Ω , pelo seu equivalente de Thévenin.
No Prob. 5.21, substitua a rede à direita dos terminais c - d pelo seu equivalente de Thévenin e use o resultado para calcular v .
Substitua o circuito à esquerda dos terminais a - b pelo seu equivalente de Thévenin, e use o resultado para calcular v .