Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 74

74- Para a ponte mostrada na Figura 4.140, determine a carga R L para a transferência de potência máxima e a potência máxima absorvida pela carga.

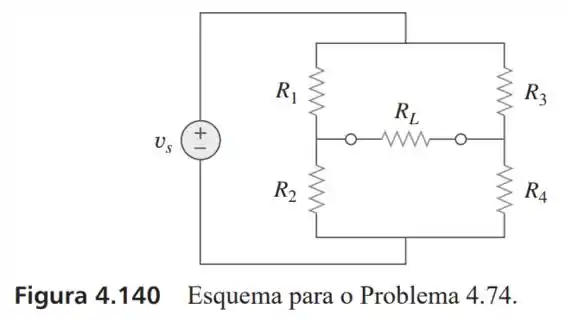
Passo 1

Vamos retirar a carga R L e a fonte independente para calcular a resistência de Thévenin desse circuito.

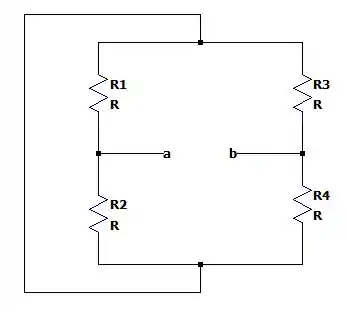
Arrumando o desenho dessa malha resistiva teremos:

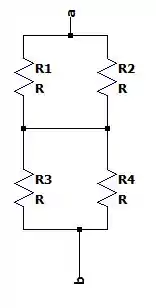
Com isso a resistência de Thévenin fará:

R t h = 1 1 R 1 + 1 R 2 + 1 1 R 3 + 1 R 4 = R 1 R 2 R 1 + R 2 + R 3 R 4 R 3 + R 4 = R 1 R 2 R 3 + R 1 R 2 R 4 + R 1 R 3 R 4 + R 2 R 3 R 4 ( R 1 + R 2 ) ( R 3 + R 4 )

E essa resistência é a resistência que se colocada em R L puxará toda a potência do circuito do enunciado.

Passo 2

Agora vamos encontrar a tensão em a e b   pela seguinte figura abaixo.

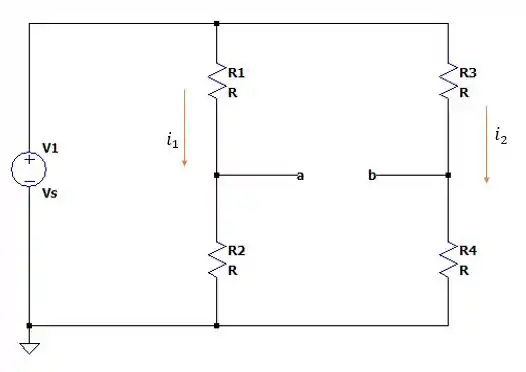
Dessa forma o valor de i 1 e de i 2 serão iguais a:

i 1 = V s R 1 + R 2 ;     i 2 = V s R 3 + R 4

Então os valores de v a   e v b serão:

V s - v a = V s R 1 R 1 + R 2 → v a = V s 1 - R 1 R 1 + R 2

V s - v b = V s R 3 R 3 + R 4 → v b = V s 1 - R 3 R 3 + R 4

Então:

V t h = v a - v b

V t h = V s 1 - R 1 R 1 + R 2 - V s 1 - R 3 R 3 + R 4 = V s R 3 R 3 + R 4 - R 1 R 1 + R 2

V t h = V s R 3 R 1 + R 3 R 2 - R 3 R 1 - R 4 R 1 R 1 + R 2 R 3 + R 4 = V s R 3 R 2 - R 1 R 4 R 1 + R 2 R 3 + R 4

Passo 3

Dessa forma a potência máxima será:

p m a x = V t h 2 4 R t h

p m a x = V s 2 R 3 R 2 - R 1 R 4 R 1 + R 2 R 3 + R 4 2 4 × R 1 R 2 R 3 + R 1 R 2 R 4 + R 1 R 3 R 4 + R 2 R 3 R 4 ( R 1 + R 2 ) ( R 3 + R 4 )

Arrumando a cara desse treco aí.

p m a x = V s 2 R 3 R 2 - R 1 R 4 2 4 ( R 1 R 2 R 3 + R 1 R 2 R 4 + R 1 R 3 R 4 + R 2 R 3 R 4 ) R 1 + R 2 R 3 + R 4

E esse é o valor da potência máxima nesse circuito. Questão literal é meio brabo, mas com calma é sempre de boa.

Resposta

R t h = R 1 R 2 R 3 + R 1 R 2 R 4 + R 1 R 3 R 4 + R 2 R 3 R 4 ( R 1 + R 2 ) ( R 3 + R 4 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

79- Obtenha o equivalente de Thévenin do circuito da Figura 4.123 usando o Pspice ou Multisim.
78- Use o Pspice ou Multisim para solucionar o Problema 4.52 .
72- ( a ) Para o circuito na Figura 4.138 , obtenha o equivalente de Thévenin nos terminais a - b . ( b ) Calcule a corrente em R L = 8Ω ( c ) Determine R L para a máxima potência que pode ser liberad
75- Para o circuito da Figura 4.141 , determine o valor de R tal que a potência máxima liberada para a carga seja de 3m W .
71- Para o circuito da Figura 4.137 , que resistor conectado entre os terminais a - b absorverá a potência máxima do circuito? De quanto é essa potência?